女妇髙潮xxxxxxyz,淑蓉第二次找卫老止痒,边做奶水边喷h高h共妻,祥仔视觉

 兩種有非圓輪的行星傳動機構的不同設計

6.1概述

單激波推桿減速器的激波器廓形一般使用偏心圓，多激波推桿減速器的激波器廓形是非圓弧曲線。當去掉推桿，內外滾子合而為一時，推桿減速器就變成了滾柱活齒減速器，如圖6.1所示。因而可以把它們都看作是非圓行星傳動機構。這類活齒傳動機構的瞬時傳動比是個常數，如式（2.8）所示，這也是設計活齒傳動機構必須遵循的準則。從后面的分析可知，這就決定了活齒傳動機構各嚙合副的運動性質都不可能是純滾動。因而要在推桿兩端加裝內外滾子以增加滾動成份而減小滑動成份。對于滾柱活齒減速器來說，因為滾柱同時要與激波器、內齒圈相接觸，所以一定有一面有滑動。因而可以說活齒傳動是一種滑滾運動方式的非圓行星傳動。由于運動副是滑滾運動，實際機構不能使用輪齒進行傳動，而是靠相嚙合的兩個輪的光滑表面接觸。
如果去掉瞬時傳動比為常數這個前提，根據運動副都作純滾動的運動方式，可設計出純滾動的非圓行星齒輪傳動機構（圖6.2）。從后面的分析可知，這種機構，相鄰兩行星輪之間的中心角是變化的，相鄰行星輪和太陽輪、內齒圈之間所包容的面積也是變化的，利用這一特性，可制造出低速大扭矩液壓馬達。

 

心角的變化規律進行了分析。

6.2節曲線之間的關系

設太陽輪節曲線方程為T₁= T₁（θ），行星輪節曲線是半徑為T₂的圓，根據機構作純滾運動或瞬時傳動比為常數這兩種不同的設計原則，可設計出兩種不同的內齒圈齒廓曲線。
6.2.1純滾動運動方式的節曲線關系

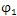
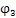
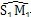
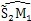
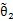
建立如圖6.3所示的坐標系，在起始位置，分別與太陽輪、行星輪以及內齒圈固聯的三個動坐標系的極軸x₁ 、x₂、x₃在同一條直線上，且指向相同。圖6.3所示為太陽輪相對行星輪轉過了 角的情形。設此時內齒圈相對該行星輪轉過的角度為 ，根據三心定理，作平行平面運動的三個構件的三個瞬心必然位于同一條直線上，而純滾動副的接觸點就是它們的瞬心。因而太陽輪與行星輪節曲線的接觸點M₁，行星輪與內齒圈節曲線的接觸點M₂以及傳動中心O₁這三個點位于同一條直線上。因為是純滾動，圖6.3中弧長 與 應相等（在起始位置S₁與S₂重合）。由此可得圖6.3中 與θ₁的函數關系為。

設μ為太陽輪節曲線在M₁點的切線正向與矢徑O₁M₁的夾角，由微分幾何知：

將（6.5）式及（6.9）式聯立，便是內齒圈節曲線的方程。同理，若已知內齒圈節曲線方程，仿上可求得太陽輪節曲線。

6.2.2按傳動比為定值的設計

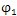
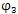
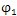
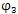
如圖6.4所示，設太陽輪相對行星輪從初始位置轉過 角時，內齒圈相對該行星輪反向轉過的角度為 。令 與 的比值為常數i₁₃，這時上一節中弧長相等的特性已無法保證，因而接觸點M₁、M₂也不再是運動的瞬心，M₁、M₂及中心O₁不一定在同一條直線上。這就是滾柱活齒傳動的結構形式。設計方法與第二章類同。現簡要敘述如下：

曲線向徑與切線正方向的夾角μ以及工作角a₁的計算都與純滾動動方式下相同，即：

若用l₁表示行星輪與太陽輪的中心距O₁O₂，則由圖6.4可得：

聯立（6.15）式及（6.18）式，便是內齒圈的齒廓方程。內齒圈的齒廓曲線是行星輪節曲線的外包絡線。
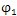
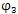
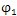
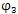
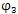
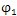
從上述求內齒圈齒廓方程的過程可以看出，由于規定了轉角 與 的比值為常數i₁₃，使得對于太陽輪的任一轉角 ，相應地有確定的值 = /i₁₃。同時圖6.4中行星輪工作角a₂也隨之由（6.12）式確定下來。因而M₁、M₂與O₁三點肯定不會始終保持在同一條直線上。其理由如下：
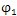
假設圖6.4中O₁、M₁、M₂三點始終都能保持在同一直線上，則對于太陽輪轉角 ，圖6.4中的a₂可根據圖6.3中的行星輪轉角θ₂求得，由圖中幾何關系及（6.4)式應有

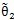
                             a₂= -a₁-θ₂=π-2μ-a₁                        （6.19）

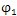
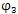
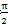
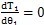
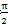
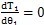
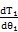
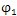
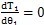
另一方面，由于 與 的比的比值為常數i₁₃，a₂的值已由（6.12）式確定。比較(6.19)式與（6.12）式可知，只有在a₁=0且μ= 時，它們才是一致的，由（6.10）式及（6.11）式知，只有在 時才有μ= ，且a₁=0，由于太陽輪的節曲線是周期性，所以在一周內只有2n₁個點（n_l是太陽輪節曲線的周期數）有 ，其余各點 都不為零，對于太陽輪的轉角 只要不是對應于 ，式（6.19）與式（6.12）是矛盾的，也就是說M₂點必然不會與M₁、O₁位于同一直線上。這說明當傳動比為常數時，行星輪與太陽輪、行星輪與內齒圈所組成的兩個嚙合副不可能都作純滾運動，一定有一個嚙合副有滑動，因而活齒傳動都是滑滾運動。

6.3節曲線的封閉條件及等分

對于作純滾運動的非圓行星齒輪傳動機構，上面求得的節曲線關系只是一般的公式，要設計出實際的非圓行星齒輪傳動機構還要受到許多限制。
6.3.1節曲線的封閉條件
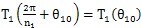
為了能夠連續轉動，已知的太陽輪節曲線當然應是連續而封閉的,T₁(θ₁）必須是θ₁的周期函數。設太陽輪一轉中的周期數是n₁，當太陽輪相對行星輪從θ₁= θ₁₀轉過一個周期時，由于 ，所以由（6.2）式可知轉動前后在接觸點具有相同的μ值。根據（6.4）式，設θ_1­­=θ₁₀時，行星輪的轉角有關系式

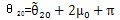
                                                        （6.20）

則當太陽輪相對行星輪轉過一個周期后，由于μ值相同，行星輪轉角關系式為：

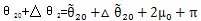
                                          （6.21）

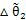
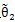
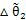
上式中△θ₂及 分別為行星輪轉角θ₂及 在太陽輪從θ₁=θ₁₀轉過一個周期后的增量。由（6.20）式和（6.21）式可知在太陽輪轉過的任一周期中，行星輪轉角增量△θ₂與 相等，即：

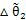
                          △θ₂=                                     （6.22）

由此可得到結論：太陽輪節曲線在一個周期內的弧長與內齒圈節曲線在一個周期內的弧長相等。若內齒圈的周期數為n₂，則n₂應大于n₁。為了減小行星輪尺寸，應取最小整數值n₁+1作為內齒圈節曲線的周期數，從而可由（6.9）式得到內齒圈節曲線的封閉條件為：

6.3.2節曲線上輪齒等分的限制

設齒輪的模數為m，為了使太陽輪、行星輪及內齒圈都有等分的輪齒，它們的節曲線都必須是周節mπ的整數倍。由上節知道，太陽輪節曲線與內齒圈節曲線在一個周期內的弧長相等，并且內齒圈的周期數比太陽輪的周期數大1，所以內齒圈節曲線的周長是太陽輪節曲線周長的（n₁+1）/n₁倍。因此只要太陽輪節曲線在一個周期內的弧長能夠被周節等分，就能保證內齒圈的等分。也就是說，設Z₁為太陽輪齒數，則Z₁應是n₁的整數倍，且太陽輪與內齒圈的輪齒等分條件為：

由于每個周期的弧長都是相等的，太陽輪節曲線的總長等于n₁個周期的弧長之和，用n₁乘以（6.24）兩邊，可得等分條件的另一種表達形式：

對于節曲線為圓的行星輪，輪齒等分條件為：

             2T₂=mZ₂                                    （6.26）

上式中z₂為行星輪的齒數，顯然內齒圈齒數z₃為：

6.3.3不干涉條件
設計的非圓行星齒輪傳動機構還應保證太陽輪最大向徑處的齒頂與內齒圈錄小向徑處的齒頂不發生相碰。若太陽輪節曲線在θ₁=0時向徑取得極小值，則內齒圈節曲線向徑的極小值為T₁（0）+2T₂，對于關于極軸有對稱性的太陽輪節曲線，在θ₁=π/n₁時有極大向徑，若齒頂高為h_a，則不發生運動干涉的條件為：

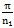
                   2T₂+T₁（0）>T₁（ ）+2h_a                    （6.28）

6.4傳動特性分析

6.4.1太陽輪與行星輪的平均傳動比
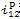
固定內齒圈，當太陽輪起點從初始位置開始轉動到與行星輪重新在初始位置接觸時，太陽輪轉過的圈數與行星輪公轉過的圈數之比 稱作太陽輪與行星輪的均傳動比。圖6.5(a）為初始位置，圖6.5(c）為太陽輪按順時針方向相對行星輪1轉過一個周期后的情形。此時內齒圈相對該行星輪也應轉過一個周期，即行星輪1從初始位置公轉過的角度為：

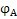
而太陽輪相對內齒圈轉過的角度 為：

即太陽輪轉兩圈零一個周期，行星輪公轉一圈。

6.4.2行星輪的個數

設太陽輪起點從初始位置相對內齒圈轉過一個周期，從圖6.5(a）轉到圖6.5(b）位置。從圖6.5(b）可知，此時在內圈的初始位置S₃處可放入另一個行星輪，稱它為2號行星輪。類似當太陽輪從初始位置相對內齒圈轉過第二個周期，在S₃可放入第3號行星輪，太陽輪旋轉一圈，放入第n₁+1號行星輪，太陽輪轉兩圈，放入第2n_l+l號行星輪，當太陽輪轉兩圈零一個周期，恰好第1號行星輪回到S₃點。所以可安放的行星輪總數為2n₁+1個。
6.4.3相鄰兩行星輪之間的中心角
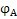
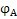
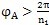
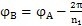
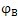
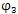
設太陽輪起點從初始位置相對內齒圈順時針轉過了 角，當 大于太陽輪一個周期（ ）時，第2號行星輪也相對內齒圈極軸公轉過了一個角度（圖6. 5（C））。令 ，則 表示此時太陽輪與2號行星輪的初始接觸點S₁₁相對內齒圈初始位S₃轉過的角度。用 表示1號行星輪相對內齒圈初始位S₃公轉過的角度，由圖6.3可得：

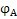
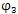
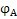
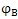
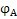
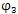
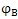
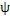
根據（6.33）式，可由任給的 確定出太陽輪起點S₁至1號行星輪與太陽輪節曲線的接觸點M₁所來的中心角θ₁，然后代入（6.30）式，可得l號行星輪中心O₂與內齒圈初始件S₃所夾的中心角 ()。用 代替（6.33）式中的 ，將解得的θ₁值代入（6.30）式，便可得到第2號行星輪中心與內齒圈S₃點所夾的中心角 ()。兩行星輪之間的中心角 為：

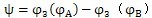
                                                   （6.34）

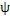
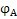
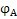
可見兩行星輪所夾的中心角 是太陽輪相對內齒圈轉角 的函數，它隨著 值的不同而呈周期性的變化，并圍繞 瞬時傳動比i₁₂為：

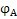
i₁₂也是隨太陽輪轉角 變化的函數。由于太陽輪和內齒圈都是非圓的，而相鄰兩行星輪之間的中心角又是變化的，因而太陽輪、內齒圈與相鄰兩行星輪之間包含的面積也是變化的，正是利用這些特性，可制造出低速大扭矩液壓馬達、空氣壓縮機等機器。

6.5設計步驟及計算實例

現以太陽輪是一個回轉中心在幾何中心的標準橢圓為例，來說明純滾動非圓仃雖傳動非圓行星傳動機構的設計方法步驟。

給定齒輪模數m=2.5,n₁=2，內齒圈周期數為3 ，設計步驟如下：

6.5.1確定齒數

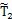
太陽輪的齒數Z₁可根據所要求的太陽輪的大小來確定，它應是n₁的整數倍。本例選z₁=42，由（6.27）式，內齒圈齒數應為z₃=63。為了確定z₂的合適數值，可以采用這樣的方法，假想太陽輪和內齒圈都退化成齒數為z₁及z₃的圓齒輪，則此時的行星輪半徑 應為：

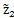
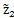
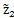
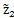
時常不是整數，我們稱它為行星輪的參考齒數。實際采用的太陽輪雖然和退化的圓齒輪具有相同的模數m和齒數z₁，但是它的形狀不是圓的，這就使得實際采用的行星輪齒數z₂應比參考齒數 小，太陽輪節曲線與圓相差越大，z₂應比 小的越多。為了減小輪齒干涉的可能生，z₂要盡量接近 。本例選z₂=10，從而得T_2­=12.5mm。

6.5.2確定太陽輪節曲線

所要求的橢圓型太陽輪節曲線方程可表示為：

上式中，a為橢圓的長軸半徑，b為橢圓的短軸半徑。由（6.25）式得輪齒等分條件為：

利用辛普生法計算數值積分，由（ 6.37）和（6.38）兩條件式組成的方程組可解算出參數a和b來，結果是：

a=59.7616   mm                    b=44.6943    mm

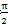
取h_a=2.5，將T₁（0）=44.6943，T₁（ ）=59.7616，T₂=12.5代入（6.28）式，可知不會發運動干涉。

6.5.3求人齒圈節曲線

根據（6.5）式和（6.9）式，可得內齒圈節曲線方程為：

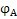
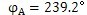
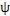
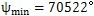
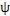
節曲線形狀如圖6.6所示。圖6.2為該輪系加上輪齒后的情形。按（6.34）式可算得相鄰兩行星輪之間的夾角隨 的變化規律，其關系曲線如圖6.7所示。由曲線圖可看出，當 時，夾角 有最小值 ，夾角 的變化范圍是2.732°。

6.5.4機構優化

從以上設計過程可以看出，根據非圓太陽輪設計行星輪為圓的純滾動非圓行經齒輪傳動機構時，并不是對任意指定的太陽輪節曲線都有解。當太陽輪節曲線的周期數n₁給定后，節曲線必須有兩個可調整的參數（例中的a和b）的要由節曲線的封閉條件及輪齒等分條件來確定。齒輪模數m和太陽輪齒數z₁是被預先指定了的。當各參數求出后，要用不干涉條件（6.28）式進行校驗，若發生干涉，應調整z₁數值，重新計算太陽輪的可調整參數。
顯然，當太陽輪與圓的差別越大時，越容易發生運動干涉。液壓馬達、空氣壓繃機等機器正是利用了相鄰兩行星輪之間的中心角變化的特點，當太陽輪與圓的差別越大時，相鄰兩行星輪之間夾角的變化范圍也越大，這是液壓馬達等機構所要求的。
令：

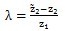
                                                                   （6.40）

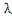
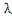
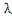
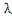
反應了非圓行星傳動機構與圓行星傳動機構的差別程度，當 =0時，非圓行星傳動機構就變成了圓行星傳動機構。 越小，越不容易發生運動干涉， 越大，相鄰兩行星輪之間中心角變化的范圍也越大。表（6.1）給出了在齒輪模數m相同的情況下，橢圓形太陽輪取不同的齒數z₁時，按上述設計步驟得到的結果。因為：

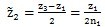
                                                       （6.41）

表6.1  橢圓太陽輪取不同齒數時的計算結果

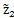
所以當z₁不能被2n₁整除時， 就不是整數。由（6.41）式和（6.40）式可得：

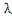
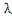
為了得到機構不發生運動干涉時的最大 值，將（6.42）式中的小于號換成等號，并將 代入，對于橢圓形太陽輪，得到下面等式：

                          mz₂=a-b+2h_a                                （6.43）

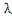
從（6.37）、（6.38）、（6.43）三式所組成的方程組中，解出a、b及z₂，將齒數代入( 6.40)便得到臨近發生運動干涉時的 值。因為z₂是整數，當m給定后，由上面三個式子所組成的方程組一般是無解的。若把m也作為一個參變數，這時方程有解。

在進行具體機構的設計時，齒輪模數m都是指定的。根據所要求設計的機構體積的大小可事先指定一個太陽輪齒數z₁的取值范圍，若以相鄰兩行星輪之間中心角變化的范圍最大為優化設計目標，按上述設計方法，并加上不干涉條件的限制．則可在所規定的z₁取值范圍內得到最佳結果。