女妇髙潮xxxxxxyz,淑蓉第二次找卫老止痒,边做奶水边喷h高h共妻,祥仔视觉

新型擺桿減速器的研究

7.1概述

擺桿減速器是一種新近提出的活齒減速器結構類型，它把沿傳動圈導槽移動的推桿變成了繞固定軸銷擺動的擺桿，使減速器中各運動副的相對運動都成為轉動，從根本上解決了現有推桿減速器移動副嚴重磨損的問題。和現有的推桿減速器或滾柱活齒減速器相比，在保持原有優(yōu)點的基礎上，使嚙合效率得到了進一步提高，是活齒減速器中較理想的一種結構形式。

文獻只提出了擺桿活齒傳動的一般結構方案，要把這種方案變?yōu)閷嶋H產品，還有許多理論問題需要解決。例如對機構傳動特性的分析，效率計算，強度校核，以及內齒圈齒廓的測量等等。本章從擺桿減速器的傳動原理著手，對這些問題進行了詳細的分析討論，為擺桿減速器的制造奠定了理論基礎。

7.2 結構組成及齒廓方程式

7.2.1結構組成

圖7.1所示為擺桿減速器的結構簡圖。擺桿減速器也由四大部分組成：激波器1；擺動機構（包括擺桿2，內滾子6, 外滾子5和軸銷7)；傳動圈3 以及與其固聯的輸出軸8；內齒圈4。可以看出，除了擺動機構外，其它構成與推桿減速器類似。也采用了兩套完全相同且互成180°的激波器及內齒圈以實現輸出的靜平衡和提高嚙合效率。

傳動中，擺桿內滾子6受到激波器驅動，而外滾子5 則與內齒圈嚙合，擺桿繞軸銷7擺動的同時，傳動圈及輸出軸轉動，從而完成了轉速的變換及功率的傳遞。

擺桿減速器的瞬時傳動比為常數，其傳動比計算完全與推桿減速器傳動比的計算公式相同。

7.2.2激波器轉角與擺桿擺動角的關系

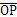
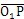
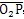
圖7.2（a）所示為激波器與擺動機構所處的初始位置，此時擺桿內滾子與偏心圓激波器的短軸端點相切接觸。O是激波器的回轉中心，P是擺桿的擺動中心，O₁及O₂分別是內外滾子中心。記R₀= ，R₁= ，R₂= ，則它們在機構轉動過程中都是不變的常量，并且：

 

上式中h₁、h₂、W₁和W_2­都是擺動中心與內外滾子中心相對位置的參數，見圖7.2（a）。

若仍記激波器半徑為T_b，激波器偏心距為e，滾子半徑為T_z，則由圖7.2（a）可得：

從上面各式可以看出，β₁、β₂及β₃都是僅和機構尺寸參數有關而與轉角無關的常量。

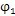
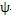
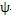
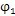
假設傳動圈固定，當激波器在驅動力矩作用下從圖7.2（a）所示初始位置按順時針方向轉過 角時，激波器與擺動機構相對位置如圖7.2(b）所示。擺動中心P點在固定坐標系（o，x，y）中的位置不變，而擺桿相應地擺過了角度 。由圖7.2(b)中△BO₁P可得 與 的關系式為：

上式中，S為P點至激波器幾何中心B點的距離：

而τ是有向角，如圖7.2（b）所示，當激波器幾何中心B點與內滾子中心O₁點分別位于直線OP兩側時，τ>0，位于同側時，τ<0

7.2.3內齒圈的齒廓方程

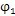
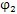
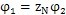
如圖7.2(b）所示，設在激波器相對傳動圈順時針轉過 角的同時，內齒圈相對傳動圈逆時針轉過的角度為 。對單激波來說， ，用p表示激波器回轉中心O至擺桿外滾子中心O₂的距離，由圖7.2(b）中△00₂P可得：

內齒圈齒廓是外滾子中心軌跡的外法向等距線，如圖7.3所示，由圖可得內齒圈齒廓與外滾子接觸點M₂在（o，x_N，y_N）坐標系下的的坐標為：

上式中，a為內齒圈齒廓在M₂點的法線與y_N軸的夾角，它等于外滾子中心軌跡在O₂點的切線正向與x_N軸正向的夾角（圖7.3）

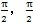
在進行具體計算時，由（7.10）式表示的a取值范圍在[- ]之內，只能使整個齒廓曲線的一部分由方程式（7.9）正確表示。為了使齒廓上所有的點都能用方程式（7.9）來正確計算，a的表示式應為：

當激波器按逆時針方向轉動時，按順時針方向轉動時的工作齒廓成了非工作齒廓，非工作齒廓成了工作齒廓。由于工作齒廓和非工作齒方是不對稱的，所以正反轉（激波器按順時針或逆時針方向旋轉）的特性也是不同的。

和推桿減速器一樣，當理論擺動機構數目比內齒圈齒數少，即Z_C=Z_N-1時，機構成為圖7.4所示的反向結構，在此結構中，擺桿外滾子中心在與內齒圈固聯的

7.3傳動特性分析

7.3.1擺桿擺動的幅度

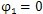
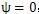
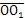
由圖7.2可知，當激波器轉角 時，擺桿處理初始位置，即擺動角度 ，此時激波器回轉中心O至內滾子中心O₁的距離 為：

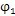
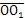
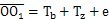
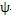
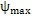
當激波器從圖7.2（a）所示初始位置順時針轉過一個角度 時， 的長度也隨之發(fā)生變化。分析圖7.2（a）可知，當 時，擺桿擺動角 取得極大值 ，此時由余弦定理可得到：

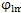
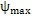
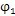
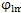
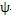
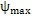
由上可知， 及 是僅與機構組成尺寸參數有關的量。當激波器轉角 從 繼續(xù)旋轉時， 便隨之從 減小，即擺動機構向內回擺，從而完成一次往復擺動。由擺動機構的運動性質決定了與外滾子相共軛的內齒圈的工作齒郭及非工作齒廓是不對稱的。

7.3.2不發(fā)生頂切的條件

設k₂為外滾子中心軌跡曲線的相對曲率，將（7.8）式中的x_o、y_o代入（2.23）式，并整理后可得

由于內齒圈齒廓曲線在齒頂處的曲率半徑最小，所以當外滾子中心軌跡曲線在齒頂處的曲率半徑小于外滾子半徑T_z時，齒廓曲線在齒頂附近將發(fā)生項切，由此可得不發(fā)生項切的條件為

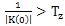
                                                            （7.30）

7.3.3同時工作的擺動機構數目
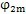
與推桿減速器類似，擺桿減速器的擺動機構只有從內向外擺動時才傳遞動力，把擺動機構從嚙合傳力開始到嚙合傳力結束推動傳動圈相對內齒圈轉過的角度叫做擺動機構工作區(qū)域角，記作 ，可表示為

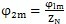
                                                          （7.31)

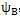
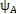
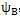
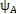
擺動機構完成一次工作循環(huán)隨傳動圈相對內齒圈轉過的角度為擺動機構工作區(qū)域角與非工作區(qū)域角之和，它等于內齒圈相鄰兩個齒所對應的中心角，記作 ，用 表示傳動圈上相鄰兩個擺動中心（抽銷）所夾的中心角，則 與 之差體現了相鄰兩擺動機構中心相對 對合初始位置的差異。從而，同時工作的擺動機構數目n_g為：

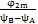
                            n_g=                                （7.32）

若擺桿減速器理論擺動機構數Z_c與內齒圈齒數有關系式Z_c=Z_N＋1，則：

 

同時工作擺動機構數目為

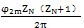
 n_g=                       （7.33）

在前面討論的推桿減速器中，推桿的工作區(qū)域角及非工作區(qū)域角是相等的，在內斷圈齒廓既不進行修形又無頂切的理論情況下，工作推桿數為推桿總數的一半。而在擺桿減速器中，擺動機構的工作區(qū)域角與非工作區(qū)域角并不相等，其工作區(qū)，或角由式（7.31）及式（7.24）確定，因而即使在內齒圈齒廓既不進行修形又無頂切，自理論情況下，工作擺動機構數目也不再是擺動機構總數的一半。根據激波器轉向的不同，工作擺動機構數目可能會超過總數的一半，也可能會少于總數的一半。

[算例]

給定擺桿減速器的下列參數：

T_b=55mm    e=5mm     R_o=87mm      T_z=10mm      Z_N=11

Z_C=12     W₁=W2=18mm h_1­=20mm     h₂=25mm

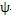
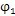
按上述公式得到齒廓曲線如圖7.1（b）所示。擺角 隨激波器轉角 變化的曲線如圖7.5所示。

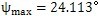
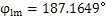
按式（7.23）計算得到 ，按式（7.24）計算得到 ，由式（7.33）計算得n_g=6.24

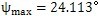
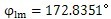
若按機構反轉計算，可得： ， , n_g=5.76

7.4效率計算

7.4.1擺動機構受力分析

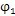
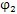
固定傳動圈，對于正向機構，當激波器順時針方向轉過 角時，內齒圈按逆時針方向轉了 角，如圖7.6所示。內滾子與激波器接觸點M₁處的法線與固家坐標系（o，x，y）的y軸夾角a₁為：

擺動機構外滾子與內齒圈齒廓接觸點M₂處的法線與固定坐標系（o，x，y）的y軸夾角a₂為：

a₂=a+

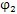
上式中a的表達式為（7.17）式。

設θ₁是內滾子與激波器之間的摩擦角，則激波器對內滾子的全反力F_J與固家坐標系（o，x，y）的y軸夾角a_J為：

                  a_J=a₁+θ₁                                             （7.37）

                   T_J=F_J 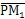sin（∠PM₁O₁+θ₂）                      （7.41）

設θ₂是外滾子與內齒圈之間的摩擦角，則內齒圈對外滾子的全反力F_N與固定坐標系（o，x，y）的y軸夾角a_N為：

                          a_N=a₂-θ₂                                （7.42）

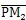
力F_N與 的夾角為∠PM₂O₂-θ₂由△PM₂O₂可得：

設f₃為擺動機構軸銷與軸承接觸面之間的摩擦系數，根據摩擦學中摩擦圓的概念可知，摩擦圓半徑P_r為

                                P_r=f_vT_P                                   （7.47）

其中T_P為軸銷半徑，f_v為當量摩擦系數，一般由實驗方法和根據某些假設業(yè)確定f_v的近似值，對于接觸面經過對磨，貼切吻合較好的跑合軸頸，取f_v=1.27f₃.

若忽略慣性力的影響，傳動圈對擺動機構的總反力F_C應該逆軸頸轉動方向切于摩擦圓。顯然F_C對P點的扭矩T_C是順時針方向，數值為：

                            T_C=1.27f₃T_PF_C                                  （7.48）

設F_C與固定坐標系中y軸的夾角為a_c，將力F_J，F_N，F_C都向P點簡化后，擺動機構受力狀態(tài)如圖7.7所示。

在忽略慣性力影響的情況下，可列出力平衡方程式為：

7.4.2效率計算

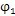
在方程組織（7.49）中，當激波器轉角 確定后，除F_J、F_N、F_C及a_C外，其它各量都相應按前述公式有了確定的數值。其中摩擦角θ₁、θ₂及摩擦系數f₃的取值，由選用的材料及潤滑情況決定。驅動力F_J可根據輸入功率求出，因而待求的未知數是F_N、F_C和a_C

從方程組（7.49）的后兩式中消去F_N，可得：

從方程組（7.49）的前兩式中消去F_N，并將所得式子中的F_C用（7.50）式代入，可得：

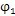
上式隱含地表達了a_c與轉角 的關系，因而可從方程式（7.51）中解出a_c來，a_c的取值范圍是0～π。若解出的a_c大于π/2時，表明圖7.7中F_e的方向為P點右上方指向P點。

下面先來進行單個擺動機構效率的計算：

仍用ω_J表示激波器轉速，則驅動功率P₁可表示為：

                 P₁=F_Jω_JL_MIsin（a_J-ε₁）                              （7.52）

上式中的L_MI表示激波器與內滾子的接觸點M₁離轉動中心O的距離，可從圖7.6

上式中L_M3­­­為傳動圈對軒動機構總作用力F_C的作用點M₃離轉動中心O的距離，如圖7.8所示。從圖中△OM₃P可得：

下面再來求機構的整體嚙合效率：

同推桿減速器類似，激波器對各工作擺動機構的作用力也可近似看作是正弦分布，即激波器對第i個處于工作狀態(tài)的擺動機構內滾子的作用力F_Ji與可能作用在擺動機構內滾子上的最大作用力F_JM的關系為：

                            F_Ji=F_JMsinδ_i                                （7.59）

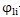
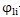
上式中的δ_i由式（7.35）計算，與激波器的位置角 也可用嚙合定位角 表示為：

總輸入扭矩等于對各工作擺動機構的驅動力矩之和，考慮到實際裝置為雙排結構，輸入功率P₁可表示為：

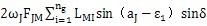
P₁=                          （7.61）

總輸出扭矩等于各工作擺動機構輸出扭矩之和，所以輸出功率P₂可一表示為：

整個機構（內齒圈固定、傳動圈輸出）的嚙合效率為：

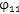
類似推桿減速器嚙合效率的計算，將嚙合定位角 在其取值范圍內取若干點進行計算，然后取其平均值作為機構的總平均效率η_P，當取的點數為20時，

7.5強度校核

根據擺桿減速器結構上的特點，強度計算應著重于激波器與內滾子之間、內齒圈與外滾子之間的接觸強度計算，以及擺動軸銷的剪切強度計算。

7.5.1激波器與內滾子之間的接觸應力

激波器與內滾子之間的接觸應力可由赫茲應力公式3.25來計算，式中激波器與內滾子之間的最大壓力F_Jmax為：

 

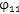
將嚙合定位角 在其取值范圍內搜索, 可求出上式的最大值。

7.5.2內齒圈與外滾子之間的接觸應力

內齒圈與外滾子之間的接觸應力可由赫茲應力公式（3.27）來計算。

從方程式（7.49）的后兩式中消去F_c，可得：

7.5.3擺動軸銷的強度

根據擺桿減速器結構上的特點，擺動軸銷主要應滿足剪切強度。軸銷的最大剪應力τ_max必須小于許用剪應力[τ]

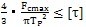
         τ_max=                                           （7.69）

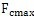
上式中 為軸銷所承受的最大壓力。

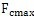
上式最大值 的求法與式（3.31）最大值的求法相同。

7.6內齒圈齒廓的公式線

盡管擺桿減速器內齒圈的工作齒廓與非工作齒廓是不對稱的，利用與前面研究推桿減速器內齒圈齒廓公法線類似的方法，仍可找出擺桿減速器內齒圈齒廓的公法線，并能進行理論長度計算和實際測量。
如圖7.9所示，AB是其中一個齒槽的一側齒廓，A′B′是跨教為K（圖中K=5)的一個齒槽的另一側齒廓。設內齒圈的齒廓曲線在圖示坐標系下可用方程式（7.9）來表示，現在來求齒廓AB及齒廓A′B′上具有的公法線。

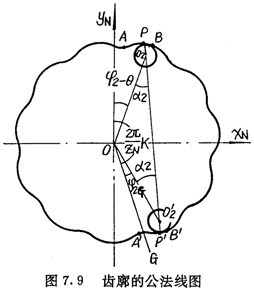
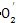
設P是齒廓AB上的一點，P點所對應的擺動機構外滾子中心為O₂點，則在齒廓A′B′上總能夠找到與P點對應的點P′，使P′所對應的外滾子中心 至中心O的距離與O₂至中心O的距離相等，即OO₂= 。
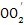
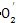
假如齒廓AB在P點與齒廓A′B′在P′點有公共的法線，則P、O₂、 以及P′這四個點必然位于同一條直線上，如圖7.9所示，從圖中△O₂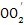 可得：
                 ∠O₂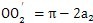                                      （7.71）

上式中的a₂是外滾子中心軌跡曲線在O₂點向徑與法線的夾角，可由圖7.3求得，為：
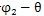
                            a₂=a+                                   （7.72）

另一方面，由圖7.9還可求得

現在先來求上式中的 ：

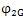
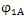
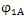
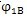
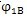
在圖7.2（b）中，若把激波器短軸（y_J）與矢徑OO₁的夾角記作 （即 =∠y_JOO₁）把固定坐標系y軸與矢徑OO₁的夾角記作 （即 =∠yOO₁），則

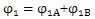
                                                  （7.74）

由圖7.2（b）可得：

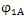
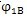
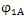
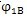
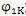
假設激波器從圖7.2（a）所示初始位置按逆時針方向旋轉到使OO₂與圖7.2（b）中OO₂長度相等的位置，如圖7.10所示，此時圖7.10中的OO₁也應與圖7.2（b）中的OO₁相等，從而圖7.10中的 、 應分別與圖7.2（b）中的 、 相等。由圖7.10可得激波器反向轉角 為：

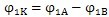
                                                  （7.76）

由式（7.74）及式（7.76）可得：

  

從而可得：

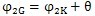
                                                      （7.78）

由式（7.71）及式（7.73）可得齒廓AB上與跨槽數為K的齒郭具有公法線的點的條件式為：

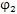
用選代法解方程（7.79），可得到齒廓AB上與跨槽數為K的齒廓A′B′具有公法線的點P所對應的外滾子位置角 ，從而可行公法線長度W_K為：

仿照分析推桿減速器內齒圈齒廓公法線數目的方法，可得到類似的結論：

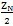
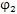
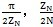
當K=INT（ ）+1時，只有一條凹齒公法線，在 位于（ ）區(qū)間測量最

大值。

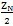
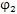
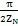
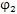
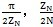
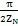
當INT（ ）≥K>K₀時，兩齒廓具有凸凹兩條公法線，在 位于[0， ]區(qū)間測量最小值，在 位于（ ]區(qū)間測量最大值。其中K_o由方程f（ ）=0解出。

從上面的分析可以看出，擺桿減速器與推桿減速器各自具有自己的特殊性：

從加工工藝上來看，對于擺桿減速器，傳動圈上的等分軸銷孔是關鍵工藝。對于推桿減速器來說，傳動圈上的徑向分布槽是關鍵工藝，應該說前者的工藝性好些。

從嚙合效率來看，擺桿減速器用轉動副代替了移動副效率增大，從而使磨損減小，有利于大功率減速器的生產。

擺桿減速器內齒圈齒形的兩側是不對稱的，從而使其正反轉特性也不相同。使功率損失減小，一側傳動性能好，一側傳動性能差。若以性能好的一側齒形為工作齒形，可設計出傳動性能優(yōu)越的單向減速器。