運動學分析
本章中,從運動學角度入手分析柔性速度補償裝置的速度輸出特性,對兩自由度連桿機構用解析法作運動學分析,再借助Matlab軟件來編程計算。運動學分析的結果將為下面的動力學分析提供理論依據。
§3.1引言
機械系統可以視為是由多個相互連接、彼此能夠相互運動的構件的組合。
在機械系統設計中有3種性質不同的分析:
(l)機械系統的運動學分析
(2)機械系統的靜力學分析
(3)機械系統的動力學分析
在本章中,暫不考慮系統的靜力學分析,先從運動學分析入手,對柔性速度補償裝置進行分析研究。主要涉及系統及其各構件的運動分析,而與引起運動的力無關。運動學分析中,系統中一個或多個構件的位置或相對位置與時間的關系是規定好的,其余構件的位置、速度和加速度與時間的關系,可以通過求解位置的非線性方程組和速度、加速度的非線性方程組來確定。
本章所要做的工作就是對上一章選出來的二自由度連桿機構,進行運動學分析,初步選定機構的結構參數,分析其輸入輸出速度能否滿足設計要求,為以后的動力學分析做依據。
§3.2Mat1ab軟件
本章里,運動學分析中,有多組比較復雜的非線性方程要解,這些都是通過Matlab來實現的。
Mat1ab目前是大家比較常用的功能強大的數學計算軟件,具有良好的開放性和運行的可靠性,在數值計算方面比較有優勢。
本章所用的Matlab,是較新的6.5版本,是一種功能強、效率高、便于進行科學和工程計算的交互式軟件包。其中包括:一般數值分析、矩陣運算、數字信號處理、建模、系統控制和優化等應用程序,并二集應用程序和圖形于同一環境,便于使用。在此環境下,所解問題的Matlab語言表述形式和其數學形式相同,不需要按傳統的方法編程。
對多數科學工作者而言,使用Matlab的庫函數的可以節省很多重復編程,節省了大量的人力、物力和時間,加快了工作進程和效率。本章要借助Matlab軟件編程來解方程。
§3.3運動學分析
平面機構運動分析的解析法也有多種,采用矢量方程解析法,比較便于應用和編程計算。
將圖2-18所示的機構簡圖,按比例繪成運動簡圖,建立直角坐標系,按照矢量方程解析法,在圖中標注各桿矢及其各桿矢的方位角。
對兩自由度連桿機構,螺旋傳動部分運動簡單,不在這里做分析,本文主要針對其余的6桿機構構成的封閉鏈,進行分析計算,建立坐標如圖3-1所示:
建立回路1矢量方程:
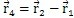
, (1)
同理,建立回路2矢量方程:
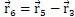
(2)
對上述兩個矢量方程式寫成標量形式的方程式,如下:
同樣,兩邊再對時間求導,整理,可得出加速度分析式:
則同理,知:
該機構本身是兩自由度機構,但是在本文中,它須滿足設計要求,即作為可調整機構,它在單自由度情況下,通過事先調整桿長比例,在第二輸入不加的的時候,也可以達到比較理想的補償效果,伺服電機電機驅動的第二輸入是起補償作用,微調桿長比例的。所以運動分析分兩種情況,一種是單自由度下的運動狀況,第二種是加入微調函數進行的運動分析。
第一種情況設曲柄輸入角速度ω=1 rad/s,第二輸入速度為零,這時相當于一個單自由度機構,螺旋傳動未起作用。機構的結構在初始狀態是完全對稱的,運用matlab編程計算,得出運動分析結果,如圖3-2所示。
首先由圖3-2可以看到,若機構結構參數設計恰當,并且調整中間滑塊3偏移到合適的位置時,可在一定范圍內,產生一個反向的速度波適度抵消原速度波動。再由圖3-3可知,在未加入第二自由度時,加速度變化值不大,說明阻力矩和電機主動力矩不會受到大的影響,不致導致原機械系統的各項參數發生大的變化。
第二種情況 第一輸入速度和第一種情況的速度值相同,現第二輸入經螺旋機構轉化為往復運動后,輸入速度為v=sinθ1(θ1為第一輸入角位移),即為滑塊3的速度,再編程計算,得出結果如圖3-4,圖3-5所示。
有上述圖3-4和圖3-5可知,引入第二自由度時,原速度波加速度波發生很大變化,這和第二自由度引入的驅動函數,有很大關系,所以應采用合理可行的控制函數,才能取得理想的速度輸出。這將為后面的控制策略提供參考。
§3.4本章小節
本章對柔性速度補償裝置的機械機構,進行了運動學分析。借助Matlab計算軟件編程解出了多組非線性方程,并分單自由度情況和兩自由度情況給出速度和加速度圖,可以直觀的看到通過柔性速度補償裝置本身產生的速度波動來抵消機械運行中產生的速度波動,為后面章節的動力學分析提供理論依據。