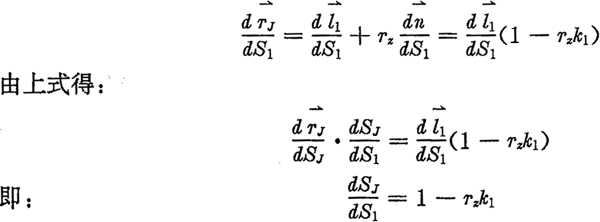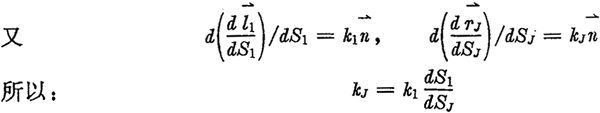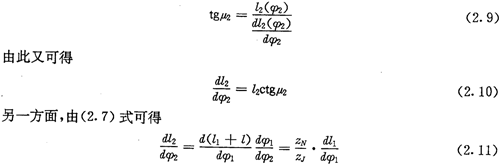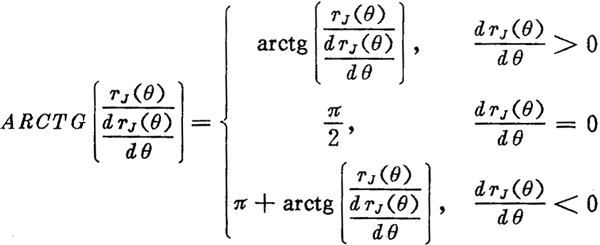2 推桿減速器的結(jié)構(gòu)分析與齒形綜合
本章根據(jù)推桿減速器的結(jié)構(gòu)特征，找出了推桿內(nèi)外滾子工作角之間的關(guān)系。這種關(guān)系不僅適用于激波器廓形為偏心圓的單激波推桿減速器結(jié)構(gòu)，而且也適用于激波器廓形為非圓弧曲線的多激波推桿減速器。利用內(nèi)外滾子工作角之間的關(guān)粵和法向等距線的幾何性質(zhì)，首次分析研究了激波器廓形為任意形狀非圓弧曲線的多激波推桿減速器的齒廓形成理論，與傳統(tǒng)的包絡(luò)法相比，具有概念清晰，所得公式形式簡單的特點，通過實例計算，證明了激波器為偏心圓的推桿減速器，其內(nèi)齒圈齒廓曲線不是擺線這一重要結(jié)論。
2.1推桿減速器的結(jié)構(gòu)及傳動比計算
推桿減速器的結(jié)構(gòu)簡圖如圖2.1所示，它由四個部分組成：1.激波器J 由輸入軸1、偏心套2、轉(zhuǎn)臂軸承3所組成。為平衡激波器所產(chǎn)生的慣性力和抵消激波器上的徑向力，一般采用雙排結(jié)構(gòu)，并使它們的相位差為180°。
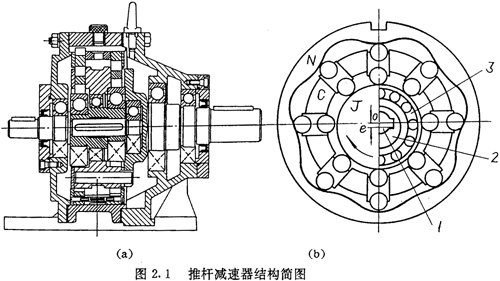
2.傳動圈C 傳動圈是一個具有雙排等分槽的構(gòu)件，它與輸出軸固聯(lián)。
3.裝有內(nèi)外滾子的推桿 內(nèi)外滾子一般是短圓柱滾子。
4.內(nèi)齒圈N 內(nèi)齒圈的齒形是與運動的推桿外滾子相共軛的曲線。與激波器對應，采用兩個完全相同的內(nèi)齒圈互成180°布置。
推桿減速器的工作原理為：當驅(qū)動力矩由輸入軸輸入后，它以等角速度、轉(zhuǎn)動，帶動偏心圓激波器繞固定中心。轉(zhuǎn)動，由于偏心圓激波器徑向尺寸的變化，激波器產(chǎn)生徑向推力，推動著推桿在傳動圈的徑向?qū)Р蹆?nèi)向外移動。推桿的徑向運動受到固定于機座上的剛性內(nèi)齒圈的約束，作用于推桿外滾子上的約束反力迫使推桿驅(qū)動具有導槽的傳動圈以等角速度ωC轉(zhuǎn)動，于是實現(xiàn)了定速比的速度變換及功率的傳遞。
在推桿減速器中，設(shè)激波器按順時針方向旋轉(zhuǎn)，則傳動圈C，內(nèi)齒圈N的轉(zhuǎn)向可能與激波器相同，也可能相反（圖2.2）。為了研究問題的方便，本文中稱傳動圈與主動件激波器轉(zhuǎn)向相同的結(jié)構(gòu)為正向結(jié)構(gòu)（圖2.2（a）)，稱傳動圈與激波器轉(zhuǎn)向相反的結(jié)構(gòu)為反向結(jié)構(gòu)（圖2.2(b))。
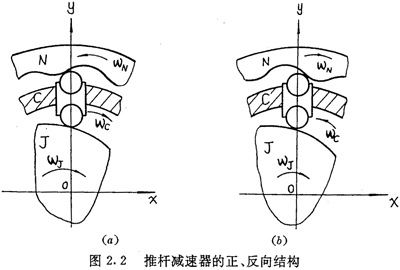
推桿減速器的正反向結(jié)構(gòu)形式完全取決于內(nèi)齒圈N的齒數(shù)zN、理論推桿數(shù)zC以及激波器J的激波數(shù)zJ。
對單激波來說，當理論推桿數(shù)zC比內(nèi)齒圈齒數(shù)zN多1（即zC=zN+l）時，推桿減速器為正向結(jié)構(gòu)（如圖2.1(b）所示）。而當推桿數(shù)zC比內(nèi)齒圈齒數(shù)zN少l（即zC=zN-1）時，推桿減速器是反向結(jié)構(gòu)（如圖1.5所示）。當推桿數(shù)zC等于內(nèi)齒圈齒數(shù)zN時，機構(gòu)不能工作，而當推桿數(shù)zC與內(nèi)齒圈齒數(shù)ZN之差在1以上（即zC＞zN+1或zC＜zN-1）時，機械也不能工作。
類似分析可得出結(jié)論：對于多激波推桿減速器，要使機構(gòu)能夠工作，齒數(shù)關(guān)系必須滿足：
ZC=ZN±ZJ （2.1）
并且ZN應是ZJ的整數(shù)倍。當式（2.1）取“+ ”號時，推桿減速器為正向結(jié)構(gòu)，取“—”號時為反向結(jié)構(gòu)。
固定激波器J、傳動圈C、內(nèi)齒圈N這三個構(gòu)件中的任何一個，而其余兩個構(gòu)件的角速度之比稱為這兩個運動構(gòu)件的傳動比。傳動比用i表示，并用下標表明相應兩個運動構(gòu)件及其主從關(guān)系。如iCN表示激波器J固定時，傳動圈C的角度速度與內(nèi)齒圈N的角速度之比值。當這兩個角度速成方向一致時，傳動比取正值，反之傳動比取負值。
利用行星齒輪傳動中確定傳動比的相對角速度法，很容易得到各種運動形式的傳動比，如表2.1表示。
上面所說的推桿數(shù)ZC是理論上的推桿數(shù)，在工程實際中，當推桿減速器要實現(xiàn)的的傳動比較大時，在傳動圈的圓周上不能夠開出理論推桿數(shù)ZC那么多的導槽，常采用“抽桿”技術(shù)，即每隔一定的間隙，抽掉一個或幾個推桿，抽桿后當然不能影響整個傳動機構(gòu)的連續(xù)運轉(zhuǎn)及傳動比。
抽桿后，機構(gòu)的實際推桿數(shù)ZC′要小于理論推桿數(shù)ZC。為了保證抽桿后受力均衡，要求抽桿是均勻的，抽桿前后推桿都是均布的。設(shè)n為每隔一個推桿所抽掉的推桿數(shù)，則實際推桿數(shù)ZC′與理論推桿數(shù)ZC的關(guān)系應為：
從推桿減速器的結(jié)構(gòu)及工作原理可以看出，由于激波器采用了滾動軸承，使得與內(nèi)滾子相嚙合接觸的激波器外環(huán)在工作過程中只是擺蕩，從而減小了與內(nèi)滾子相嚙合時的滑動摩擦。另外，只要能使外滾子轉(zhuǎn)動靈活，內(nèi)齒圈齒廓與外滾子之何的滑動摩擦也可變得很小。可見，推桿減速器中滑動摩擦以推桿與導槽之間最為嚴重。
工程技術(shù)人員在實踐中圍繞著傳動圈的結(jié)構(gòu)提出了不少改進方案。一種想法是在推植與導槽之間加放滾針，軌圖2.3所示，使移動副轉(zhuǎn)換成通過滾動體接觸的滾動副。但由于實際生產(chǎn)中工藝上的原因，這種方法沒有被采用。
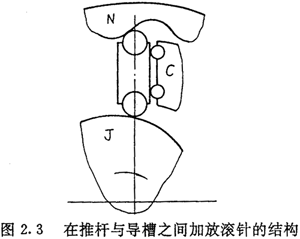
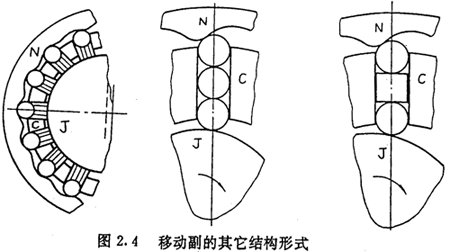
圖2.4所示是推桿與導槽所構(gòu)成的移動副的另外幾種形式，它們也未能很好地解決移動副所帶來的滑動摩擦問題。
當把推桿去掉，內(nèi)外滾子合而為一時，便是滾柱活齒減速器的結(jié)構(gòu)。還可以將激波器設(shè)計成內(nèi)工作輪廓，內(nèi)齒圈設(shè)計成外齒輪（波形輪），這種結(jié)構(gòu)稱為外波式活齒傳動結(jié)構(gòu)。
2.2內(nèi)齒圈齒廓的法向等距線及性質(zhì)
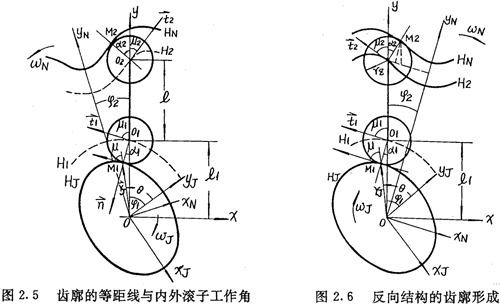
取固定坐標系（o，x，y）及分別與激波器和內(nèi)齒圈固聯(lián)的坐標系（o，xJ，yJ，）和（o，xN，yN），如圖2.5所示，它們在初始位置是重合的。
設(shè)以yJ為坐標極軸，激波器J的廓形HJ的表達式為TJ=TJ（θ），則內(nèi)滾子中心O1的軌跡H1是這樣形成的：設(shè)HJ上任意一點M1處的單位法線向量為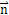
，在法線上，取長度Tz（Tz等于滾子半徑），得一點O1，則這個點就在H1上，這樣逐點形成的H1與HJ是法向等距線，它們在對應點有共同的法線。證明如下：
這表明，H1在01點處的切線向量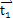
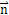與垂直，即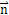既是HJ在M1點的法線，又是H1在O1點的法線，得正。
下面再推導一下齒廓及其法向等距線的相對曲率關(guān)系。設(shè)HJ的孤長參數(shù)為SJ，相對曲率為kJ，而H1的孤長參數(shù)為S1，相對曲率為k1，由微分幾何可得：
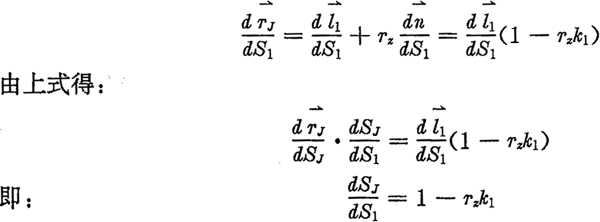
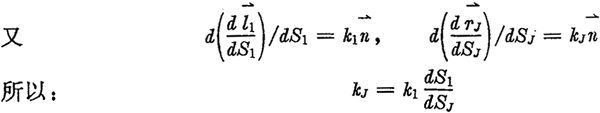
最后得到法向等距線在對應點的相對曲率關(guān)系為：
kJ=k1/（1-Tzk1） （2.3）
相對曲率半徑關(guān)系：
PJ=P1-Tz （2.4）
內(nèi)齒圈的齒廓HN與外滾子中心的軌跡H2也是法向等距線，它們在對應點也有共同的法線，相對曲率與相對曲率半徑也有和上面類似的關(guān)系。
2.3內(nèi)外滾子工作角之間的關(guān)系
設(shè)在某一時刻，激波器與內(nèi)滾子相切接觸在M1點，內(nèi)齒圈齒廓與外滾子相切接觸在M2點，如圖2.5所示，則圖中a1與a2分別叫做內(nèi)外滾子工作角。在工作行程，al及a2都為正值，在非工作行程，它們都為負值。
上面已說過，內(nèi)滾子中心的軌跡H1是激波器廓形HJ的外法向等距線，激波器按順時針方向轉(zhuǎn)動時，H1是一條以轉(zhuǎn)角φ1為參數(shù)按逆時針方向生成的有向曲線，設(shè)其方程式為：
l1=l1（φ1）
由微分幾何知，曲線Hl的向徑與切線正方向的夾角μ1可由下式計算：
切線的正方向應取與曲線極角的計量方向一致，當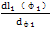
大于零時，μ1在0至π/2范圍內(nèi)取值，當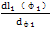小于零時，μ1在π/2至范圍內(nèi)取值。
由（2.5）式可得：
如圖2.5所示，設(shè)激波器相對傳動圈順時針轉(zhuǎn)過φ1角的同時，內(nèi)齒圈相對傳動圈反方向轉(zhuǎn)過了φ2角（對于反向結(jié)構(gòu)，內(nèi)齒圈則相對傳動圈按與激波器轉(zhuǎn)向相同的方向轉(zhuǎn)過φ2角，見圖2.6）。
外滾子中心O2的軌跡H2是內(nèi)齒圈齒廓的內(nèi)法向等距線，它可以看作是一條以φ2為參數(shù)按順時針方向形成的有向曲線（對圖2.6所示反向結(jié)構(gòu)，H2是一條按逆時針方向形成的有向曲線H2的方程為：
l2=l2（φ2）=l1（φ1）+l （2.7）
將φ1與φ2分別作為上述有向曲線H1及H2的參數(shù)，無論對于正反向哪種結(jié)構(gòu),φ2隨著φ1的增加而增加，并有關(guān)系式
同樣，由微分幾何，曲線H2的向徑與切線正方向的夾角μ2可由下式計算：
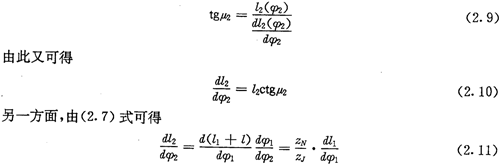
分析圖2.5及圖2.6可知，當μ1及μ2的取值在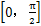
范圍內(nèi)時，a1及a2為正值，當μ1及μ2的取值在
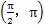范圍內(nèi)時，a1及a2為負值，故恒有下面的式子成立：
2.4.1內(nèi)齒圈的齒廓方程
為了提高加工精度及降低成本，推桿內(nèi)外滾子通常選用半徑相等的短圓柱滾子標準件，這樣，對激波器廓形和內(nèi)齒圈齒廓兩條曲線只要知道其中之一，便可根據(jù)機構(gòu)傳動比、推桿長度及滾子半徑來確定另外一條曲線。
設(shè)選定激波器廓形為TJ=TJ（θ），按通常的極坐標表示法，θ增加的方向為逆時針方向。由激波器廓形方程便確定了激波次數(shù)ZJ。設(shè)激波器相對傳動圈從初始位置順時針轉(zhuǎn)過了φ1角，對正向結(jié)構(gòu)，內(nèi)齒圈相應地相對傳動圈逆時針轉(zhuǎn)過了φ2角（圖2.5)，對于反向結(jié)構(gòu)，內(nèi)齒圈相應地相對傳動圈順時針轉(zhuǎn)過了φ2角（圖2.6),由圖可得：
上式中的μ為曲線HJ在M1點的向徑與切線正方向的夾角。前面已說過，曲線向徑與切線正向的夾角μ的取值范圍是［O，π]。在用計算機解算時，反正切函數(shù)arctg（x）的值域是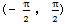
，所以為了使概念明確和使用方便，特定義下面在本文中使用的函數(shù)：
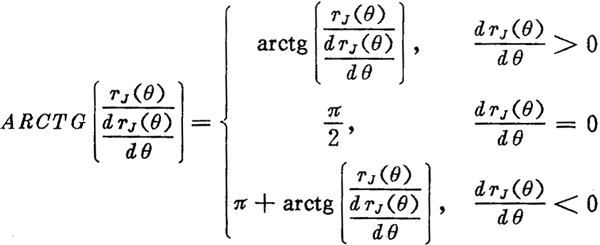
上式中TJ（θ）表示極徑，其值當然為正。
上一頁
下一頁
