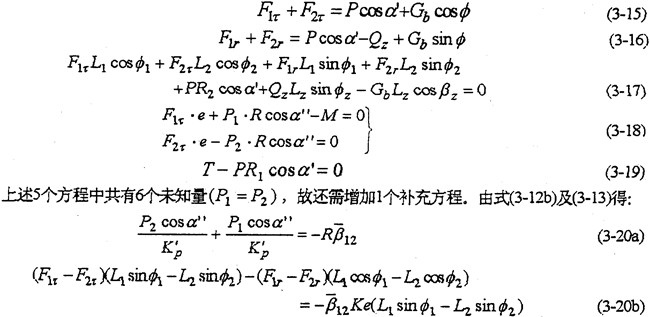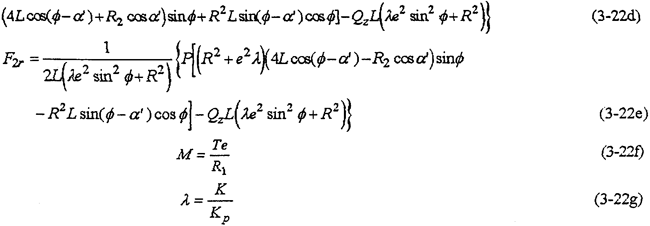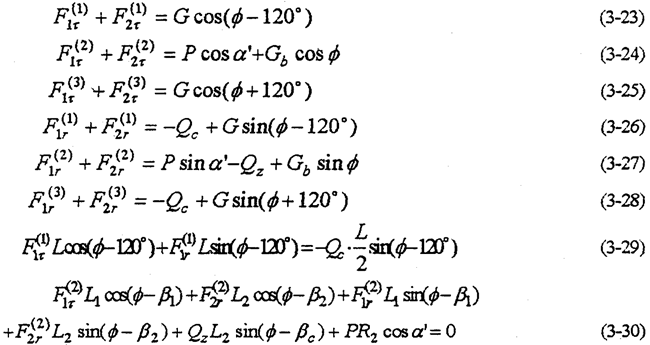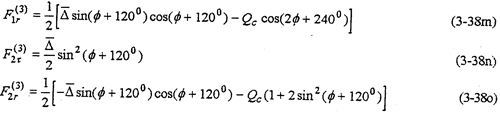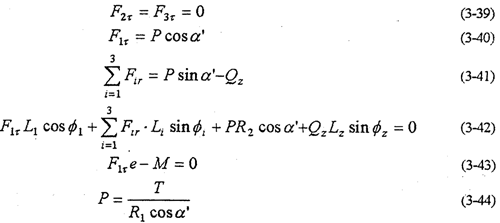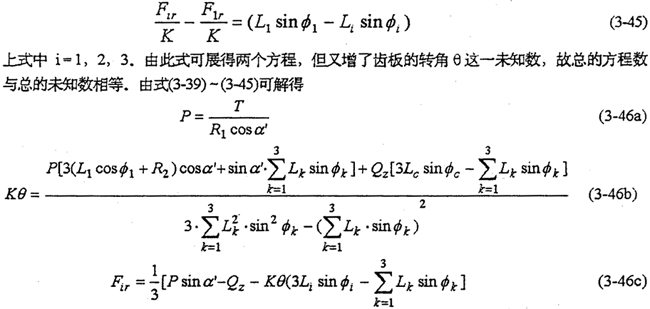3.4一齒環內齒行星傳動動力分析模型
一齒環內齒行星傳動按機構克服“死點”的方法,有雙軸式雙軸輸入、雙軸式單軸輸入、以入多軸式等結構形式。
3.4.1雙軸式雙軸輸入一齒環內齒行星傳動
這種輸入形式是通過一套定軸傳動機構將動力分流,傳遞到兩根高速軸上,形成雙軸輸入。具體結構見圖1-6及圖3-2。由動力分析基本方程式(3-1)~(3-5)令m=2,N=1得
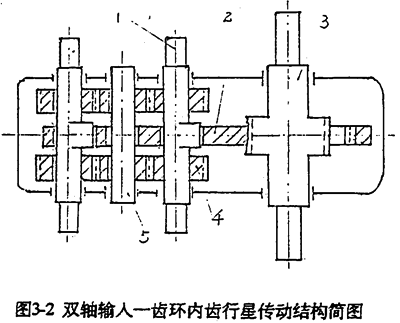
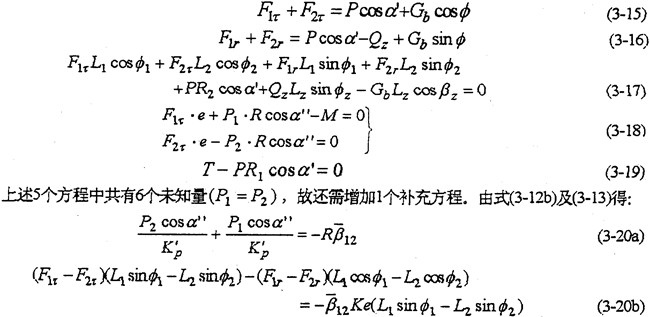
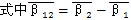
由方程式(3-15)~(3-19)和(3-20)可以完全確定雙軸輸入式的一齒環內齒行星傳動機構的動力參數。各動力參數中除嚙合力只與負載大小有關外,其余載荷均與傳動機構的幾何參數L1,L2,β1,β2,R1,R2,α′,α″等因素有關。故可以通過調整這些參數,以達到滿足結構、載荷要求。
當β1=π,β2=0,L1=L2=L時,為高速軸對稱于輸出軸兩則布置,若不計各構件重力,則解為


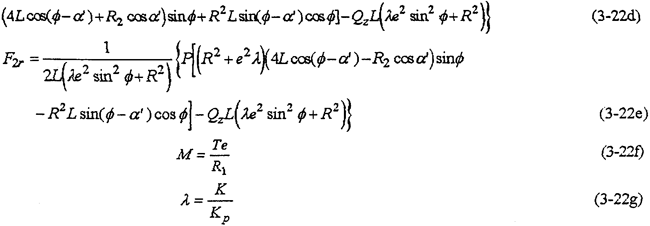
由以上兩種情況的解式(3-21)及式(3-22)可知,內齒行星傳動機構的行星軸承載荷與軸承接觸剛度K及分流機構齒輪的接觸剛度Kp有關。分流機構既傳遞動力又傳遞運動,使機構在任何時候都具有確定的運動,沒有機構的死點位置,這從各解的結果可以看看無論φ怎么變,各載荷值均不會出現無窮大情況。
3.4.2多相并列雙曲柄機構一齒環內齒行星傳動
以三相并列雙曲柄機構一齒環內齒行星傳動機構為例(見圖1-3圖3-3),帶行星齒板的雙曲柄機構與另外兩套雙曲柄機構相位差互為120°。疫帶行星齒板轉動的相位角為φ,則另兩相雙曲本機構的相位角為φ-120°及φ+120°由動力分析基本方程,取P(1)=P(3)=0,P(j)=P得
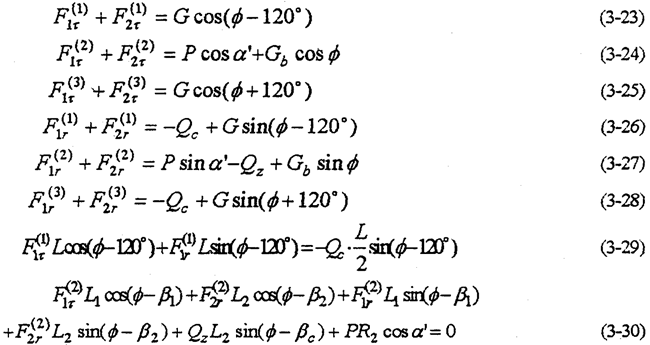
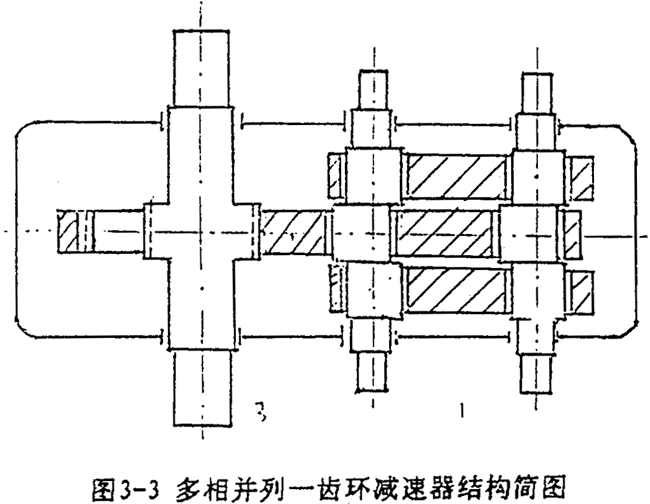


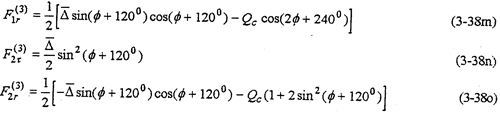
3.4.3多軸式一齒環內齒行星傳動
多軸式一齒環內齒行星傳動機構是在行星齒板平內采用三根或者三根以上不在同一直線上分布的高速偏心軸(曲柄),支承內齒行星輪(齒板)。當任意二個偏心軸與齒板組成的雙曲柄機構,絕對不會處于運動不確定的死點伴置,當它們一起運動時,相互推動,整個機構就不會出現運動不確定的位置。這類內齒行星傳動機構見圖1-9,圖1-10所示等多軸機構的結構形式。除輸入軸曲柄有未知輸入力矩M外,其余曲柄均認為是二力構件。以三軸式機構為例,由動力分析基本方程,令m=3,N=1得
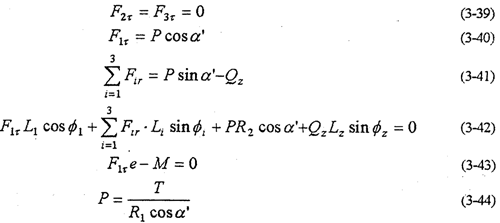
該機構的靜不定次數S=1,故需增加一個補充方程,才能完全確定機構的各動力參數。由齒板位移協調方程式(3-14)得
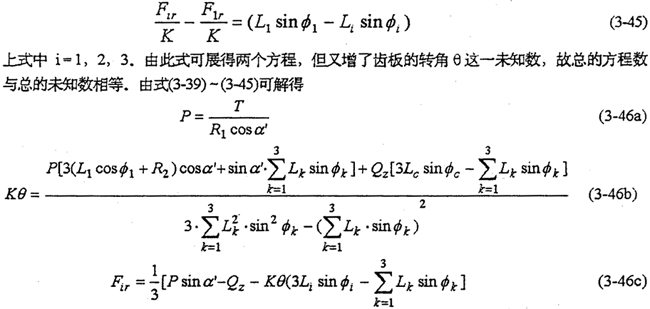

上一頁
下一頁