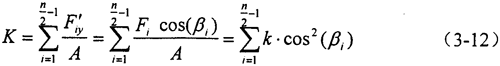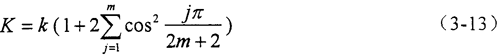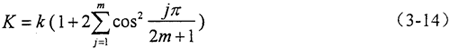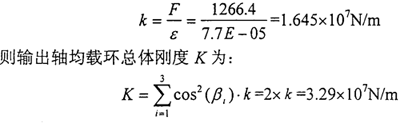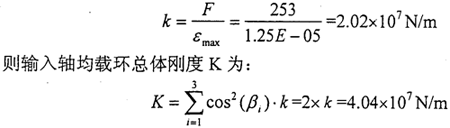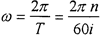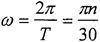3.5彈性均載環靜力學分析
3.5.1彈性均載環的約束及載荷
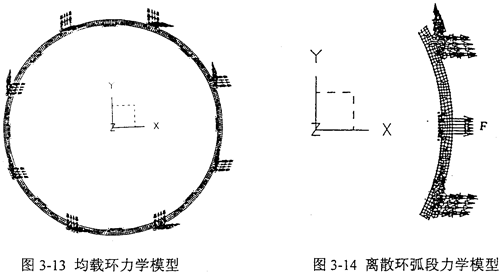
合理地確定彈性均載環的約束及載荷,是正確進行彈性均載環靜力學和動力學分析的關鍵。由于均載環置于輸入軸和輸出軸的軸承外圈和軸承座孔之間,軸承座和箱體是一體,箱體固定在工作臺上,所以邊界條件取為均載環的八個外凸臺固支,作用力F作用在內凸臺表面上。均載環的力學模型如圖3-13所示。彈性均載環的內外表面分別均勻分布八個凸臺。為了便于有限元分析,可以將均載環離散成八個環弧段,每個環弧段由一個內凸臺和其相臨兩個外凸臺之間的部分構成,內凸臺受徑向載荷,離散環弧段與均載環的載荷和邊界條件相同。離散環弧段力學模型如圖3-14所示。
3.5.2用彈性力學的方法求解均載環的剛度
彈性力學是固體力學的一個分枝,主要研究物體(彈性體)由于受外力作用或溫度改變以及支座沉陷等原因而產生的應力、形變和位移,彈性力學對彈性體作較精確的分析。對于本文的離散均載環弧段,環弧段的厚度h<<它的長度2L(或寬度2B),且撓度較小,可以利用彈性力學中薄板的小撓度變曲理論,將均載環結構參數與剛度聯系起來,通過正確處理邊界條件來改善計算結果。離散環弧段的計算模型如圖3-15所示,假定環弧段的支承邊界條件為兩端固支。
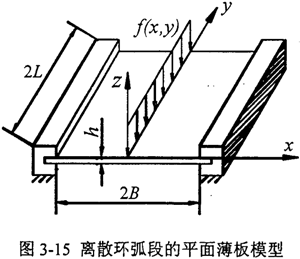
圖中f(x,y)=F·δ(x)/2L為環弧段單位面積上的分布力。
式中 F——環板內凸臺受力;
δ(x)=Dirac——力分布函數。
按照平面薄板的小撓度彎曲理論,薄板變形的控制方程為:
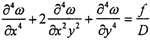
式中 D=Eh2/((12(1-μ2))為薄板的抗彎剛度;
h——薄板厚度;
μ——薄板材料的泊松比;
E——薄板材料的彈性模量。
邊界條件取為:

上式為兩端固支的環弧段剛度的計算公式,如將支承邊界條件改為一端簡支和一端固支或兩端簡支,則相應的環弧段剛度為兩端固支剛度75%或50%。由式(3-8)可知,彈性均載環的厚度對其剛度的影響最大;在彈性均載環平均直徑一定時,凸臺尺寸及承載寬度對其剛度有一定影響。
由上述的輸入軸均載環的實際結構參數,可以求出輸入軸均載環環弧段的剛度為:
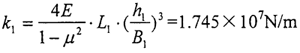
由上述的輸出軸均載環的實際結構參數,可以求出輸出軸均載環環弧段的剛度為:
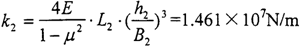
3.5.3用有限元方法求解均載環的剛度
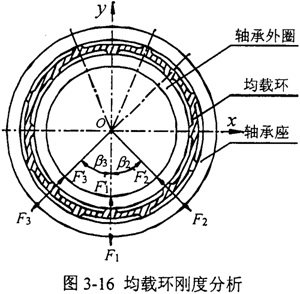
由3.5.1可知,將均載環離散成八個環弧段,每個環弧段由一個內凸臺和其相臨兩個外凸臺之間的部分構成,均載環剛度與其離散環弧段剛度之間的關系如圖3-16所示。
彈性均載環的剛度定義:均載環中心所作用之力與環的中心在該力方向上位移之比。對于4m+4型、內外表面均勻分布n個凸臺的均載環,若軸心沿-y方向有徑向位移A,則軸承外圈受到均載環下半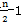 個內凸臺的支反力Fi′(i=1,2,……,
個內凸臺的支反力Fi′(i=1,2,……,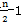 )作用,將均載環視為以外凸臺中線為界的n個環弧段的組合,則均載環相應下半
)作用,將均載環視為以外凸臺中線為界的n個環弧段的組合,則均載環相應下半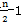 個環弧段內凸臺的徑向變形為:
個環弧段內凸臺的徑向變形為:
Ai=A·cos(βi) (3-10)
式中 βi——各弧段方位角,i=1,2,……,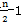 。
。
一般來說,由均載環結構的對稱性可知其各離散環弧段具有相同的剛度k,于是各離散環弧段的支反力為:
Fi′=k·Ai=k·A·cos(βi) (3-11)
式中 k——環弧段剛度,單位為N/m,i=1,2,……,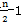 。
。
由均載環剛度定義,均載環總體剛度為:
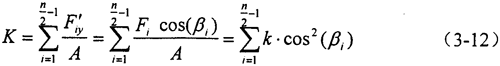
式中Fiy′——Fi沿y方向的分力,i=2,……,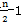 。
。
所以,對于n=4m+4類型的彈性均載環,總體剛度K與環弧段剛度k之間的關系可用下式表示:
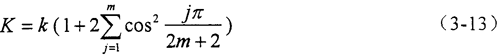
對于n=4m+2類型的彈性均載環,它具有雙向剛度異性,總體剛度K與環弧段剛度k之間的關系可用下式表示:
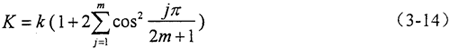
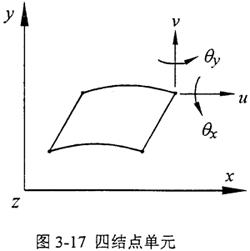
由上述分析可知:均載環離散成八個對稱的環弧段,因此均載環總體剛度的計算歸結為求解其離散的環弧段的剛度。本章利用I-DEAS分析軟件計算內、外表面各均勻分布八個凸臺的輸入、輸出軸彈性均載環的離散環弧段的剛度,從而得到均載環的總體剛度。對于圖3-15所示的離散環弧段,內凸臺的受力沿+x方向,并且在沿軸向方向上均勻分布,所以只需考慮xy平面內的形變分量和位移分量即可,可以認為是平面應力問題。在單元選擇上,選用“平面應力問題”中的四結點單元,定義單元的四結點厚度與彈性均載環的寬度相一致。四結點單元如圖3-17所示。
對于輸出軸均載環,為了補償前述的等效中心誤差ymax,在實際分析時,當圖3-15所示的離散環弧段的最大位移形變ε=ymax=0.077mm時,選用平面應力問題求解,根據均載環的實際結構,設置單元類型、大小及材料特性,選取四邊形單元,單元長度選為0.4mm,對于輸出軸均載環,由Meshing模塊生成四邊形單元3499個,節點4495個;均載環八個外凸臺固支,建立約束集和解集,則可運用I-DEAS分析軟件Model Solution模塊計算得到環弧段內凸臺受力F=1266.4N,力F均勻地分布在內凸臺表面上。
此時離散環弧段的應力σ為:
σmin=6.49E-13MPa
σmax=3.74E+02MPa
由于均載環離散為八個對稱環弧段,故整個輸出軸均載環的最大應力就等于離散環弧段的σmax。均載環的材料為55Si2Mn,由機械工程手冊查得:它的抗拉強度σb≥1.274E+03MPa,遠遠大于σmax,所以足夠滿足強度要求。
并且可以求出離散環弧段的剛度k:
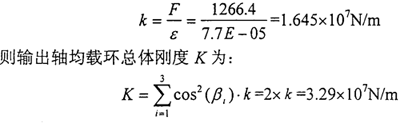
對于輸入軸均載環,它的受力來源于一級傳動的載荷分配不均勻力。由一級傳動齒輪受力分析可知,假定一級傳動載荷分配不均勻系數KP=1.50,則可得載荷分配不均勻力F=253N,力F均勻地分布在內凸臺表面上。選用平面應力問題求解,根據均載環的實際結構,設置單元類型、大小及材料特性,選取四邊形單元,單元長度選為0.4mm,對于輸入軸均載環,由Meshing模塊生成四邊形單元1954個,節點2394個;均載環八個外凸臺固支,建立約束集和解集,則可運用I-DEAS分析軟件Model Solution模塊計算得到環弧段的位移為:
εmin=0
εmax=1.25E-O2mm
此時離散環弧段的應力σ為:
σmin=8.43E-O2MPa
σmax=1.4IE+O2Mpa
由于均載環離散為八個對稱環弧段,故整個輸入軸均載環的最大應力就等于離散環弧段的σmax。均載環的材料為55Si2Mn,由機械工程手冊查得:它的抗拉強度σb≥1.274E+03MPa,遠遠大于σmax,所以足夠滿足強度要求。
并且可以求出離散環弧段的剛度k:
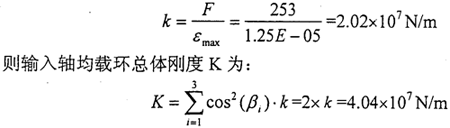
用平面薄板的小撓度理論計算得到的環弧段的剛度比用I-DEAS軟件計算得到的環弧段的剛度要小約13.6%,因此在精度要求允許的情況下,可以用理論計算預估均載環的剛度,用來指導設計。
3.6彈性均載環動力學分析
機器中的傳動部分是機器的基本組成部分,機械傳動系統的優劣直接影響著機器性能的發揮。隨著機械傳動速度的提高,機械振動和平衡問題已經成為某些機械設計中的關鍵問題。各種機械在工作過程中所產生的振動,可使它們的動態性能嚴重惡化,從而降低其傳動精度、生產效率、機械零件的壽命,甚至引起機械零件的破壞。同時,由于機械振動所產生的噪音,又可污染生產環境,影響人們健康。因此,動力學分析已經成為機械設計的必要手段。
動力學分析是指在已知系統的動力學模型(數學模型)、外部激振力和系統工作條件的基礎上,分析研究系統的動力特性。動力學分析大致包括下列三方面的問題:
1.固有特性問題;
2.動力響應問題;
3.動力穩定性問題;
對于本文的均載環來說,作為減速機的一個子結構,它不可能產生自激振動。因此,在本章中只研究均載環的固有振動頻率、模態振型和動力響應。求解多自由度有阻尼離散系統動力學問題,通常建立模型的運動方程,采用模態分析法和子空間迭代法,用高級語言編程求解系統受任意激振力作用下的固有頻率和模態振型。在本章中,考慮到彈性均載環的運動方程難以建立,故而采用有限元方法來進行動力學分析。
3.6.1彈性均載環的固有特性
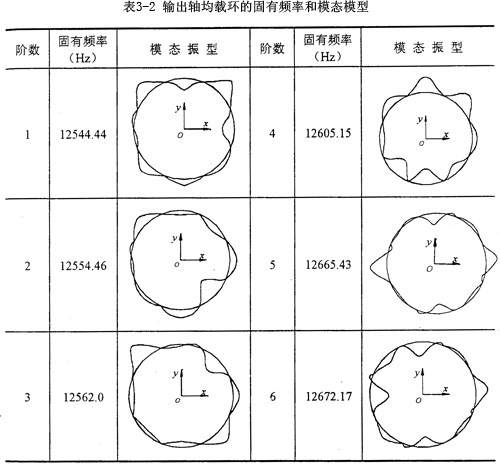
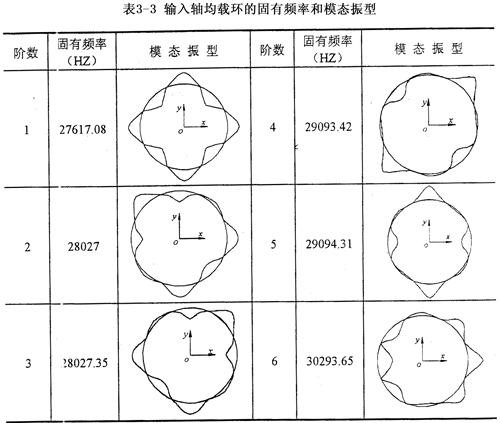
本文利用I-DEAS軟件來進行彈性均載環的動力學分析。首先求解均載環的固有特性問題,在圖3-14所示的均載環的力學模型中,均載環的邊界條件取為均載環的八個外凸臺固支,輸出軸均載環和輸入軸均載環的有限元模型參數同3.5.3,中研究的一致。應用Model草藥Solution模塊中的Model response部分,選用Normal Mode Dynalnics-SVI(普通模態動力分析——同步矢量迭代法)方法求得輸出軸均載環和輸入軸均載環的前六階固有頻率和模態振型分別如表3-2、3-3所示。
由表3-2可知,輸出軸均載環的前六階固有頻率在1250OHz~12700Hz之間,這些固有頻率遠遠高于三環減速機的轉動頻率和嚙合頻率,三環減速機幾乎沒有發生共振的可能性。由振動理論可知,構件的約束增多,尤其是固定約束增多,則它的固有頻率將增大。本文中的輸出軸均載環由于固定約束點較多而導致它的固有頻率較高。
由表3-3可知,輸入軸均載環的前六階固有頻率在2750OHz~30300Hz之間,這些固有頻率遠遠高于三環減速機的轉動頻率和嚙合頻率,三環減速機幾乎沒有發生共振的可能性。本文中的輸入軸均載環由于固定約束點較多而導致它的固有頻率較高。
3.6.2彈性均載環的動力響應
首先求解輸出軸均載環的動力響應問題,輸出軸均載環的外部激振力來源于少齒差內嚙合的載荷分配不均勻力F,由前述分析可知,考慮三環減速機主要制造安裝誤差,當離散環弧段的最大位移形變ε=ymax=0.077mm時,則可運用I-DEAS分析軟件Model Sofution模塊計算得到離散環弧段的內凸臺受力F=1266.4N。力F均勻地分布在內凸臺表面上。
載荷分配不均勻力F來源于三環減速機少齒差傳動中的嚙合力,嚙合力的方向總是相切于齒輪的基圓,指向嚙合點,在嚙合的過程中,嚙合力的方向總在周期地變化著。于是可得:在某一時刻具有n個內、外凸臺的輸出軸彈性均載環內凸臺所受的載荷為:
Fi=F·cos(βi)
式中 βi為各內凸臺與F力作用點之間的夾角,i=1,2,……,n;
通過對嚙合力的分析,認為輸出軸均載環受到簡諧激振力Fcos(ωt)是合理的,其中ω為輸出軸的回轉角速度。根據傳動關系可得:
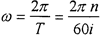
式中 T——輸出軸回轉周期;
n——輸入電機轉速。
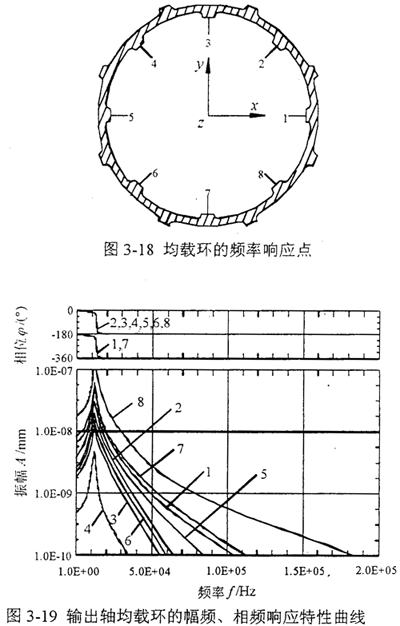
取輸出軸均載環的八個均布內凸臺的中間點作為振動響應點,示意圖如圖3-18所示。取輸出軸均載環系統粘性阻尼系數c=0.03,均載環的邊界條件取為均載環的八個外凸臺固支,輸出軸均載環和輸入軸均載環的有限元模型參數同3.5.3中研究的一致。于是應用I-DEAS分析軟件Model Solution模塊中的Model Response部分,可以求得彈性均載環的暫態激勵幅頻、相頻響應特性曲線如圖3-19。
同時可以救是輸出軸均載環的動態撓度和動態主應力的最大值分別為:
ydmax=7.91E-05mm<[yd]
σdmax=1.43E-01MPa<[σd]
式中 [yd]——輸出軸均載環許用動態撓度,本章中取[yd]=0.4mm;
[σd]——輸出軸均載環許用動態主應力,本章中取[σd]=700MPa。
所以說:輸出軸均載環的動態特性良好。
其次求解輸入軸均載環的動力響應問題,輸入軸均載環的外部激振力來源于定軸傳動的載荷分配不均勻力F,由一級傳動齒輪受力分析可知,假定一級傳動載荷分配不均勻系數KP=1.50,則可得三環減速機的載荷分配不均勻力F=253N。
載荷分配不均勻國F來源于三環減速機定軸傳動中的嚙合力,嚙合力的方向總是相切于齒輪的基圓,指向嚙合點,在嚙合的過程中,嚙合力的波動總在周期地變化著。于是可得:在某一時刻具有n個內、外凸臺的輸入軸均載環內凸臺所受的載荷為:
Fi=F·cos(βi)
式中 βi為各內凸臺方位角,i=1,2,…,n。
通過對嚙合力的分析,認為輸入軸均載環受到簡諧激振力Fcos(ωt)是合理的,其中ω為輸入軸的回轉角速度。根據傳動關系可得:
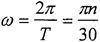
式中 T——輸入軸回轉周期;
n——輸入電機轉速。
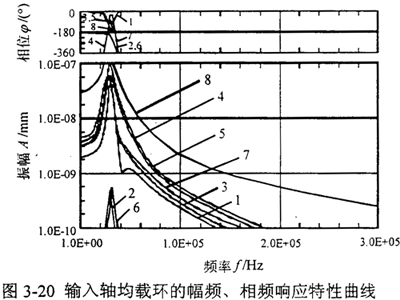
取輸入軸均載環的八個內凸臺的中間點作為振動響應點,示意圖同圖3-18所示。取輸入軸均載環系統粘性阻尼系數c=0.03,均載環的邊界條件取為均載環的八個外凸臺固支,輸出軸均載環和輸入軸均載環的有限元模型參數同3.5.3中研究的一致。于是應用I-DEAS分析軟件Model Solution模塊中的Model Response部分,可以求得輸入軸均載環的暫態激勵幅頻、相頻響應特性曲線如圖3-20所示。
同時可以求得輸入軸均載環的動態撓度和動態主應力的最大值分別為:
ydmax=1.42E-10mm<[yd]
σdmax=1.81E+00MPz<[σd]
式中 [yd]——輸入軸均載環許用動態撓度,本章中取[yd]=0.04mm;
[σd]——輸入軸均載環許用動態應力,本章中取[σd]≥700MPa。
所以說:輸入軸均載的動態特性良好。
3.7本章小結
本章在對三環減速機的制造安裝誤差和載荷分配進行深入分析的基礎上,結合行星傳動均載的原理,提出了一種新型的利用零件彈性變形均載的三環減速機均載機構一金屬彈性環均載機構,并且對其進行靜力學和動力學分析,從理論上驗證均載環的均載效果。
衡量三環減速機載荷分配性能的指標是載荷分配不均勻系數KP,本章提出了一種利用非線性有限元方法一間隙單元法計算三環減速機載荷分配不均勻系數KP的方法,并對兩種三環減速機進行了實例計算。載荷分配不均勻系數KP的確定不僅為三環減速機的載荷分配提供理論依據,而且為三環減速機均載機構的設計提供評價依據。
對彈性均載環進行靜力學分析,用彈性力學平面薄板的小撓度分析理論和有限元分析的方法分別計算輸入軸均載環和輸出軸均載環的剛度和強度。
對彈性均載環進行動力學分析,利用I-DEAS分析軟件對三環減速機的輸入鐘均載環和輸出軸均載環進行了動力學分析,得到其前六階固有頻率、模態振型和瞬態激勵頻率響應特性曲線。
綜上所述,金屬彈性均載環具有較好的位移均載效果,能夠滿足位移均載要求,是一種理想的三環減速機均載機構。
上一頁
下一頁



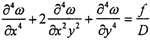

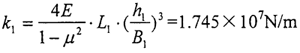
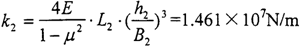
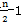 個內凸臺的支反力Fi′(i=1,2,……,
個內凸臺的支反力Fi′(i=1,2,……,