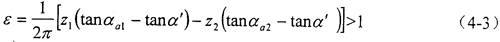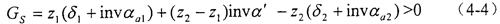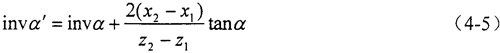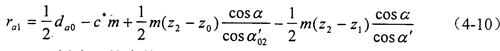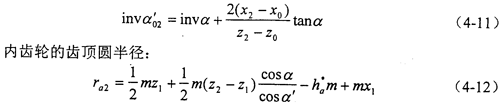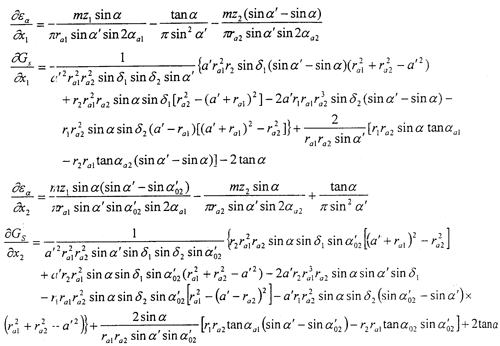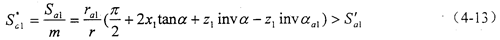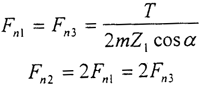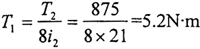第4章 三環減速機的設計
4.1引言
三環減速機是在少齒差行星傳動的基礎上,為了適應現代機械設備對傳動裝置的要求而誕生的新型減速機。三環減速機由于其原理的獨特性,因而對于它的設計也提出了新的適應性要求。本章在前述理論分析的基礎上,對三環減速機的設計進行了研究,力求在傳動結構和技術參數上,使三環減速機的優越性得以充分實現。
三環減速機的設計包括兩個關鍵部分一少齒差內嚙合部分和均載裝置部分的設計。對于少齒差內嚙合部分,主要是嚙合的內、外齒輪變位系數的確定,本章推導了用插齒刀加工的少齒差內嚙合變位系數的牛頓迭代公式,較好地解決了這個問題;對于均載裝置部分,主要是均載形式的確定和對該種形式的研究,第三章提出一種金屬彈性均載環作為三環減速機的均載裝置來實現均載和減振,并對均載環進行有限元和動力學分析,驗證其具有適宜的剛度、足夠的強度、能夠滿足位移均載的要求;三環減速機屬于行星傳動裝置,因而它的安裝也要滿足行星傳動裝配條件,本章將對三環減速機的裝配條件進行深入的探討。本章還對三環減速機的兩個關鍵零件一內齒環板和偏心套進行有限元應力分析,指導進行合理的設計。三環減速機的設計還包括其它一些部分一箱體部分、輸入輸出軸部分等等,限于篇幅,這些部分在本章中不加以討論。
三環減速機的兩個關鍵零件一內齒環板和偏心套的加工也是不容忽視的問題,由于三片內齒環板必須同時插齒加工且滿足180°相位差,因此要求內齒環板工裝要有準確的定位;偏心套是三環減速機的薄弱環節,它的制造也應引起足夠的重視。限于篇幅,三環減速機的制造在本章中不加以討論。
4.2三環減速機的設計
4.2.1少齒差內嚙合的兩個主要限制條件
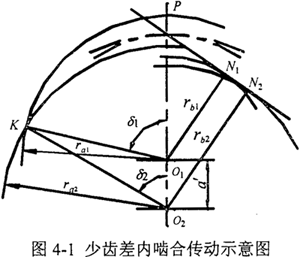
少斷差內嚙合傳動是指內、外齒輪的齒數差較少的一種行星傳動形式,它具有傳動比大、體積小、重量輕、加工方便等優點,日益廣泛地應用于國防、礦山、冶金、化工、紡織、起重運輸、建筑工程、食品工業和儀表制造等部門和行業中。少齒差內嚙合傳動示意圖如圖4-1所示。
在設計內嚙合齒輪傳動時應注意如下幾點:
1.為了保證漸開線齒廓,內齒輪的齒頂圓必須大于基圓,即
da2≥db2 (4-1)
2.為了避免輪齒的磨損,內齒輪的齒頂不得變尖,齒頂厚度必須大于(025~0.4)m,即:
Sa2>(0.25~0.4)m (4-2)
3.切制內齒輪時必須避免范成頂切和徑向切入頂切現象
4.必須保證內嚙合齒輪副的重合度ε>1。即
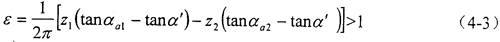
5.必須保證不產生齒頂干涉和齒廓重迭干涉,應使GS>O。即
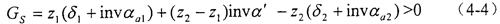
少齒差內嚙合傳動由于內、外齒輪的齒數差少,易于產生各種干涉。在設計和實際使用中只需滿足以下兩個主要限制條件:
1.按嚙合中心距a′裝配時,保證齒輪副不產生齒廓重迭干涉;即應滿足齒廓不重迭干涉系數GS>GS′。
2.保證獲得足夠的重合度,即應使齒輪副的重合度εa>εa′。
其中εa′,GS′分別為設計要求的少齒差內嚙合的重合度和齒廓不重迭干涉系數。
4.2.2少齒差內嚙合變位系數的確定
在少齒差內嚙合傳動中,目前使用最廣泛的行星齒輪和中心齒輪的加工方法是范成法。外齒輪大都采用螺旋形的齒輪滾刀在Y38型或Y312型滾齒機上切制而成。內齒輪通常是采用插齒刀在Y54型或Y58型插齒機上插制而成。
變位系數的確定是少齒差內嚙合傳動設計的關鍵。文獻中所述的內、外齒輪都按滾齒加工的計算公式推導出的變位系數的迭代公式,與內齒輪插齒、外齒輪滾齒的實際加工情況不一致,雖然能夠保證給定的重合度和齒廓不重迭干涉系數的要求,但是不能保證標準頂隙,而且一般得出的嚙合角也比較大。本章推導了少齒差內嚙合傳動實際加工情況的變位系數的迭代公式,解決了上述問題。
少齒差內嚙合傳動的兩個主要限制條件是否滿足,取決于齒輪的有關參數,這些參數包括齒數z0,z1,z2、齒形角α、齒頂高系數ha*,ha0*、頂隙系數c*、變位系數x0,x1,x2等。由內嚙合齒輪副的無齒側間隙嚙合方程:
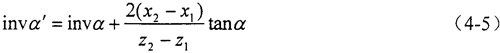
式中 α——齒形角,一般取α=20°;
α′——嚙合角;
z1、z2——分別為外、內齒輪的齒數;
x1、x2——分別為外、內齒輪的徑向變位系數。
可得:在z1、z2和α一定時,變位系數xl和x2的變化直接影響到嚙合角α′的大小,嚙合角是變位系數的函數;而選擇變位系數xl、x2的問題,實質上是決定內嚙合齒輪副是否能夠消除干涉現象。對于一對嚙合齒輪,可把變位系數視為自變量,而把其余的參數作為常量,即限制條件是變位系數的函數。因此,滿足兩個主要限制條件的問題便歸結為求合適的變位系數的問題。
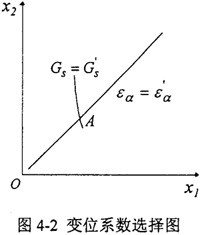
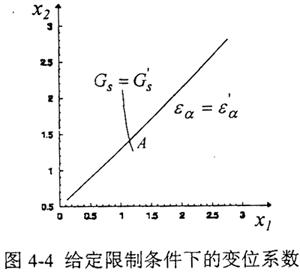
某項限制條件,可以曲線的形式表示在xl,x2坐標系內,若把每個限制條件都以曲線形式繪于x1,x2坐標系內,則它們的交點A便對應著這對齒輪的變位系數,如圖4-2所示。
由于限制條件中有許多是超越方程,直接求解變位系數非常困難或是不能求解。因此,本文將討論如何用逐步逼近的迭代方法來求得同時滿足兩個主要限制條件的變位系數x1和x2。
少齒差內嚙合的重合度計算公式為:

把變位系數x1,x2取作獨立變量,把嚙合角α′取作中間變量,用牛頓法求解。其迭代程序為:

其中εα′,GS′分別為設計要求的少齒差內嚙合的重合度和齒廓不重迭干涉系數。
應用上述公式迭代時,參考機械工程手冊,只要初始值(x1(0),x2(0))選得接近精確解(x1,x2),迭代過程就會收斂。
外齒輪的齒頂圓半徑:
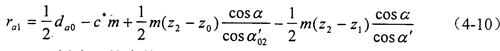
式中 z0,x0——插齒刀的齒數、變位系數;
da0——插齒刀z0的齒頂圓直徑,da0=m(z0+2ha0*+2x0);
ha0*——插齒刀的齒頂高系數與頂隙系數之和;
a02′——插齒刀加工內齒輪時的嚙合角。
內齒輪與插齒刀的無側隙嚙合方程為:
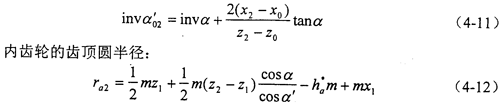
借助于Mathenatica軟件,推導出行列式元素為:
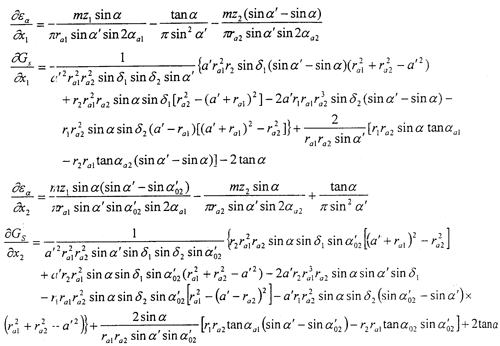
按照迭代過程求得的x1,x2是否滿足設計要求,尚需檢驗變位外齒輪的齒頂厚系數,驗算如下:
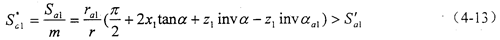
式中 Sa1′——設計要求的最小的外齒輪的齒頂厚系數。
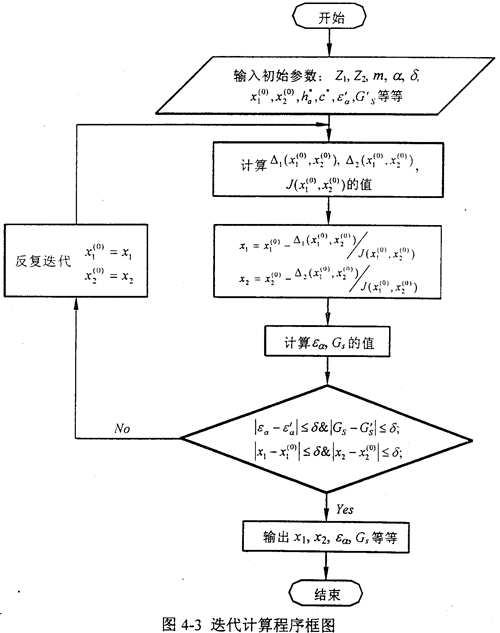
根據上述公式推導,編制了迭代計算程序,程序框圖如圖4-3所示。
對于本文的實驗樣機HITSH145,內嚙合齒輪副的參數為:z1=42,z2=44,m=3.5,ha*=0.8,ha0*=1.1,c*=0.3,α=20°,z0=22,x0=0.126,則可應用上述迭代公式求得當取εα′≈1.05及 GS′≈0.05時的外、內齒輪變位系數x1和x2。
按照文獻中所述的內、外齒輪都按滾齒刀計算的迭代公式,最后得到的計算結果如下所示:
x1=1.433 x2=1.722
α′=38.192° εα=1.05
GS=0.05 c=1.377mm
a=4.185mm
并且驗算外齒輪齒頂厚系數得:
Sa1*=0.546
給定初值x1=1.0、x2=1.5,迭代過程及迭代結果如表4-1所示。
按照本文所述的內齒輪為插齒、外齒輪為滾齒的加工方法的迭代公式,最后得到計算結果如下所示:
x1=1.142 x2=1.407
α′=37.356° εα=1.05
GS=0.05 c=c*m=1.05mm
a′=4.138mm
并且驗算外齒輪齒頂厚系數得:
Sa1*=0.874
給定初值x1=1.0、x2=2.0,迭代過程及迭代結果如表4-2所示,給定限制條件下的變位系數選擇如圖4-4所示,交點A便對應著這對齒輪的變位系數x1=1.14204,x2=1.40742。
表4-1 按滾齒刀計算的迭代過程及迭代結果
| 迭代次數 |
第一次 |
第二次 |
第三次 |
第四次 |
第五次 |
| 變量 |
x1 |
1.64556 |
1.43467 |
1.43340 |
1.43339 |
1.43339 |
| x2 |
1.89802 |
1.72276 |
1.72248 |
1.72247 |
1.72247 |
| 迭代結果 |
εa |
0.999404 |
1.037740 |
1.050295 |
1.05 |
1.05 |
| GS |
0.610248 |
-0.050981 |
0.046851 |
0.049992 |
0.05 |
| c |
1.731905mm |
1.320847mm |
1.375545mm |
1.377092mm |
1.377092mm |
| α′ |
43.94741° |
36.89975° |
38.15867° |
38.19207° |
38.19207° |
| Sa1* |
1.218750 |
0.282717 |
0.544335 |
0.545879 |
0.545892 |
表4-2 滾齒刀計算的迭代過程及迭代結果
| 迭代次數 |
第一次 |
第二次 |
第三次 |
第四次 |
第五次 |
第六次 |
| 變量 |
x1 |
1.11301 |
1.14312 |
1.14215 |
1.14205 |
1.14204 |
1.14204 |
| x2 |
1.33214 |
1.40130 |
1.40740 |
1.40740 |
1.40742 |
1.40742 |
| 迭代結果 |
εa |
1.06348 |
1.06606 |
1.05024 |
1.05000 |
1.05000 |
1.05 |
| GS |
1.45340 |
-0.08768 |
-0.03195 |
0.04880 |
0.04993 |
0.05 |
| c |
1.05mm |
1.05mm |
1.05mm |
1.05mm |
1.05m |
1.05mm |
| α′ |
52.2256° |
35.6077° |
37.1097° |
37.3521° |
37.3685° |
37.3562° |
| Sa1* |
0.72848 |
0.878514 |
0.87514 |
0.87430 |
0.87424 |
0.87423 |
4.2.3 內齒環板的應力分析
內齒環板是三環減速機的關鍵傳動零件,在該傳動機構中實質是一連桿,承受一定的沖擊;它又是一內齒輪,是一計算分析比較復雜的零件。其強度性能直接影響整機的運動和動態性能,因此有必要對內齒環板的應力和變形進行數值計算。對內齒環板進行有限元分析,首先應該對三環減速機在傳動過程中的受力狀況進行分析,建立曲型工況下的內齒環板的有限元計算模型;然后利用I-DEAS求出各模型的應力、變形分布及變化規律,對內齒環板強度狀況進行研究。
本文研究的HITSH145型三環減速機的內齒環板的結構和受力情況如圖4-5所示,該減速機的主要參數如表4-3所示。Ai孔軸、Bi孔軸為光孔輸入軸,O孔為內齒輪,O孔軸為輸出軸。每個內齒環板都受到三個力作用:Ai孔與配合軸間的作用力FAi、Bi孔與配合軸間的作用力FBi和O孔處的內齒輪與輸出軸上的外齒輪之間的嚙合力Fni。
表4-3 內齒環板主要參數表
| 輸入轉速n2 |
輸出扭矩T |
齒數Z2 |
內齒輪模數m |
傳動比i |
齒形角α |
壓力角α′ |
| 966r/min |
875N·m |
44 |
3.5mm |
21 |
20° |
37.356° |
三環減速機的運動和動力通過兩根相互平行且各帶有三個偏心套的輸入軸傳遞給三片內齒環板,三片環板上的內齒輪同時與輸出軸上的外齒輪相嚙合,嚙合點間的相位差為180°,把運動和動力傳遞給輸出軸。為了考慮三環減速機的慣性力和慣性力偶矩平衡,中間環板的厚度取為兩側環板厚度的兩倍。假定兩側環板傳遞總功率的四分之一,則
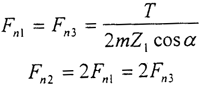
根據第二章的三環減速機的受力分析部分和內齒環板的有限元分析要求,可得內齒環板載荷工況如表4-4的上半部所示。在圖4-5中,φ為Fni力作用點與x軸正向的夾角,φA、φB分別為FAi、FBi與x軸正向的夾角。表4-4的下半部列出的是φ在12個典型位置時的Fni、FAi、FB。
根據內齒環板軸向不能竄動及Ai、Bi孔圓周對稱的特點,將約束處理為:圓周Ai、Bi的周邊沿軸向(z向)單側位移為零,同側周邊上、下、左、右極限位置處x、y方向位移為零,內齒輪O無約束。
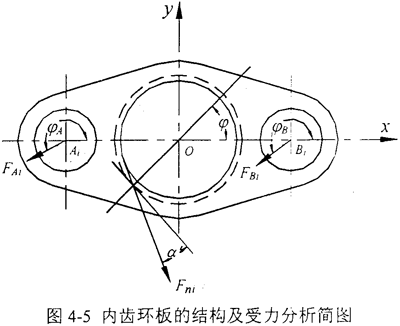
表4-4 內齒環板載荷工況表
| 載荷工況編號 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
集中
力位
置角
(°) |
內齒輪φ |
0 |
30 |
60 |
90 |
120 |
150 |
180 |
210 |
240 |
270 |
300 |
330 |
| 左孔φA |
67.0 |
86.8 |
106.5 |
126.7 |
148.4 |
173.4 |
207.1 |
259.8 |
318.3 |
356.9 |
23.0 |
46.4 |
| 右孔φB |
29.1 |
80.2 |
136.4 |
175.1 |
202.7 |
225.6 |
246.6 |
226.7 |
286.8 |
307.4 |
329.5 |
355.1 |
集
中
力
F
(N) |
內齒輪O |
Fmx |
-2403 |
-2998 |
-2790 |
-1834 |
-387 |
1164 |
2403 |
2998 |
2790 |
1834 |
387 |
-1164 |
| Fmv |
-1834 |
-387 |
1164 |
2403 |
2998 |
2790 |
1834 |
387 |
-1164 |
-2403 |
-2998 |
-2790 |
| 左孔Ai |
FAi |
2145 |
2236 |
2190 |
2010 |
1714 |
1335 |
941 |
697 |
832 |
1203 |
1597 |
1925 |
| 右孔Bi |
FBi |
959 |
735 |
858 |
1206 |
1582 |
1897 |
2110 |
2198 |
2153 |
1980 |
1694 |
1331 |
根據三環減速機內齒環板的實際結構,設置單元類型、大小及材料特性,內齒環板的分析屬于空間問題,選取四面體單元進行計算,選取單元長度為3mm,由Meshing模塊共生成實體線性的四面體單元11658個,節點12170個,內齒環板的有限元網格如圖4-6所示。12種載荷工況下各模型的約束處理都是相同的,由此建立了內齒環板在12個典型嚙合位置時的有限元分析模型。建立約束集和解集,利用I-DEAS軟件Model Solution模塊對建立的12個有限元模型分別求解,可求出12種載荷工況下各模型的位移及應力如表4-5所示。12種載荷工況下內齒環板的最大位移如圖4-7所示,12種載荷工況下內齒環板的最大應力如圖4-8所示。
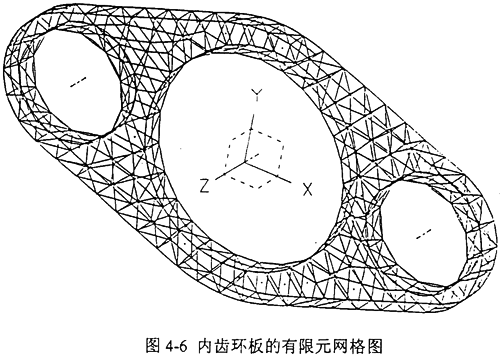
表4-5 內齒環板12種典型工況下的位移及應力計算結果
| 模型編號 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
位移δ
10-3mm |
全局值 |
Max |
16.4 |
2.83 |
3.47 |
7.64 |
7.75 |
2.37 |
1.74 |
2.81 |
3.34 |
8.19 |
7.73 |
2.57 |
應力值
σMPa |
Max |
13.5 |
9.36 |
14.8 |
12.3 |
13.9 |
9.97 |
15.0 |
10.0 |
11.3 |
13.1 |
13.5 |
10.5 |
| Min×10-2 |
1.09 |
1.81 |
2.61 |
1.76 |
1.79 |
2.32 |
6.72 |
1.44 |
3.27 |
1.88 |
3.68 |
1.33 |
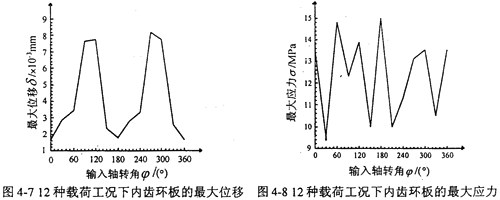
由圖4-7、4-8可知,內齒環板的應力與位移都以360°為周期變化,最大位移出現在φ=270°時的工況位置,這是因為此時的嚙合力Fni和Bi孔與配合軸間的作用力FBi都出現在φ=270°附近,它們的彎曲效應和剪切效應共同作用,出現位移的最大值點,同時也說明環板的最上部、最下部是環板位移的瓶頸環節;最大應力出現在180°+α′時的工況位置,這是因為此時的嚙合力Fni、Ai孔與配合軸間的作用力FAi和Bi孔與配合軸間的作用力FBi都出現在φ=180°附近,它們的彎曲效應和剪切效應共同作用,出現應力的最大值點,同時也說明環板內齒輪與兩個Ai孔、Bi孔的聯接部分是內齒環板應力的瓶頸環節。
4.2.4偏心套的有限元分析
在三環減速機中,高速輸入軸上要加工三對偏心軸頸,依次安裝三個環板。由于中間一塊環板的安裝比較困難,一般采用圖4-9所示的偏心套結構,高速軸1與偏心套2、3、4之間通過平鍵聯接,軸與偏心套之間為過渡配合H7/k6,而偏心套通過環板軸承5與環板相聯。
偏心套是高速輸入軸上的主要傳遞扭矩部件,由第二章分析可得,偏心距e=4.18mm,由于偏心結構和裝配位置上的限制,所以它成了三環減速機中的薄弱環節,有必要對其進行深入的分析。
對于偏心套來說,首先計算它的受力情況;假定中間環板的偏心套所受載荷為兩側環板的2倍,其它環板平均分配載荷。在額定輸出扭矩T2=875N.m下,偏心套承受的扭矩為:
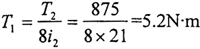
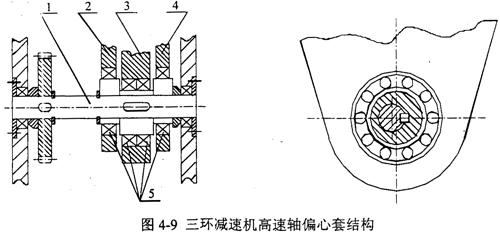
應用I-DEAS軟件,按照空間問題求解,根據如圖4-10所示的偏心套的結構,設置單元類型為四面體、單元長度為3mm及材料特性為45號鋼,由Meshing模塊共生成四面體單元3988個,節點1042個,它的有限元分析模型如圖4-11所示,由于是平鍵聯接,所以載荷均勻地作用在偏心套主動鍵槽一側;由于偏心套可以轉動。則邊界條件取為偏心套內、外兩個圓柱面z向旋轉自由。建立約束集和解集,運用Model Solution模塊求得結果如下:
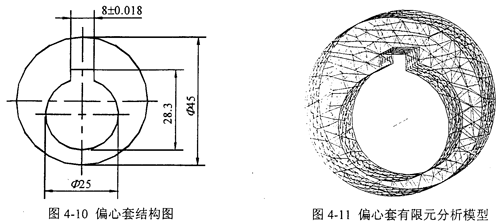
此時偏心套的位移ε為:
εmin=0;
εmax=l.43E-02mm,發生在鍵槽主動側邊。
此時偏心套的應力σ為:
σmin=2.38E-02MPa;
σmax=5.13E+01MPa,發生在鍵槽主動側邊。
偏心套的材料為45號鋼,由機械工程手冊第一卷查得:45號鋼的抗拉強度σb≥3.35E+02MPa,遠遠大于σmax,所以足夠滿足強度要求,所以偏心套在工作狀況下是安全的。
上一頁
下一頁