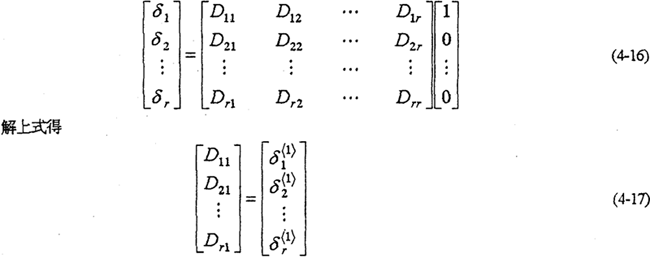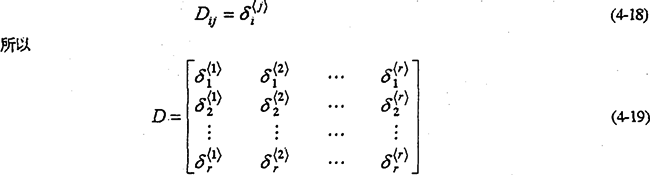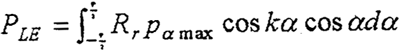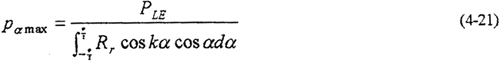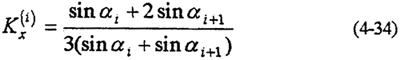內齒行星齒輪傳動零件的變形位移研究
4.1引言
上一章對內齒行星齒掄傳動機構的動力建模進行了系統的研究。從研究中發現，建立位移協調補充方程時，都必須將變形位移與構件的柔度或剛度聯系，變換成真正要求解的力或力矩的關系。對結構簡單的軸類零件以及齒輪等，可以利用現有的有關計算公式直接建立變形位移與力握）的關系。然而對于行星齒板、偏心套等零件，由于其結構形狀復雜只能將變形按接觸變形進行處理，即用接觸力與接觸剛度系數之比代換位移。這種方法簡便，可以直接導出解的結果。適合于載荷不大，零件變形小的傳動。但對于重載高速傳動來說，零件的總體變形往往比較大，特別是行星齒板的齒圈厚度是隨位置角度變化的，其變形也將隨嚙合齒變化而變化。
因此，齒板的剛度在工作過程中變化也很大，不可能為常數。行星齒板上某點的位移與作用在齒板上力（載荷）的關系并不象接觸變形那樣，某點的位移只與該點受載及該點柔度（剛度）有關。而是通過齒板的整體柔度系數矩陣聯系作用在齒板上所有外力來反映某點的位移。把這種位移與力的關系叫做柔度方程。行星齒板柔度方程中的柔度系數，隨工況位置φ(j)變化，不是固定值。柔度系數可以在不同的工況時通過有限元法等數值計算方法來確定。本章用有限元法計算行星齒板及偏心套在不同工況時的柔度系數，導出其位移與力的關系。對軸、軸承、外齒輪等零件的位移與力的關系，用現有的理論公式表示。
4.2彈性體的柔度方程及其柔度計算
柔度方程亦是彈性體的位移表達式。有限元法中的剛度方程就是彈性體節點位移與節點力之間的關系
由式（4-1）表達的是彈性體節點位移的隱函式。必須將其轉換只與彈性體外載荷有關的節點位移顯函式，才有用于內齒行星齒輪傳動的動力分析中。由于式（4-1）中的總剛度矩陣K是一個奇異矩陣，不存在逆矩陣，所以不能直接解出其位移表達式來。必須考慮實際邊界條件，以及為避免出現剛體運動，對具體的彈性體進行某體節點零位移的約束處理。即對總剛度矩陣K要作相應的變更，使總剛度矩陣變為非奇異矩陣。處理邊界位移約束的方法見參考文獻。
經過約束處理后，式（4-1）記作
式（4-6）就是彈性體離散化后，經過約束處理的節點位移表達式，即彈性體的柔度方程。設約束處理后有n組節點位移，即
式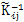
（i=1，2，…，n；j=1，2，…，n）是彈性體柔度子矩陣。
所以柔度方程為
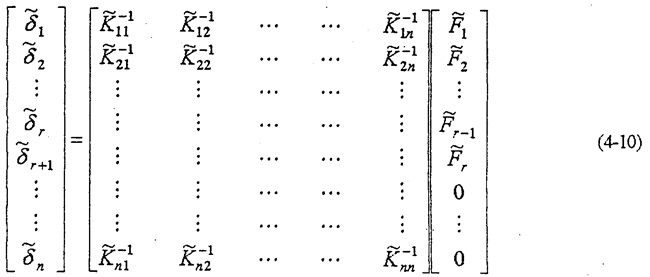
式（4-12）就是外力作用點位移及其作用力的關系式。
柔度矩陣戌構件的材料、幾何形狀以及劃分網格形狀等因素有關。其中各元素可以依次加單位載荷，用式（4-12）計算確定。先令式（4-14）中F1=1，F2=F3=…=Fr=0代入式（4-12）得
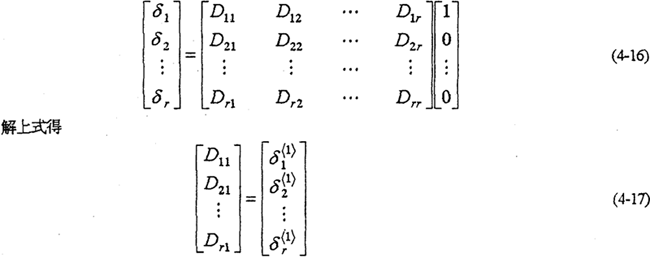
上式中Di1=δ<1>i就是F1作用點加單位載荷計算出的柔度系數值。同理可分別在F2，F3，…，Fr作用點加單位載荷，求出其余的柔度
系數值，于是得到
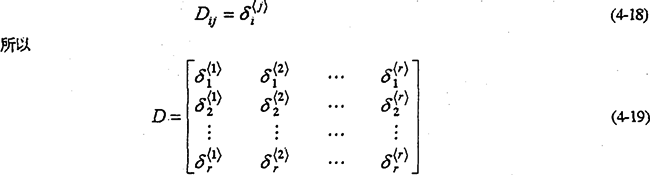
式（4-19）就是用有限元法通過加單位載荷求得的彈性體柔度矩陣
4.3偏心套及行星齒板的柔度計算
從上節介紹知，彈性體的柔度系數矩陣可以通過有限元法，加單位載荷來計算確定。因此，偏心套及內齒行星傳動齒板的柔度計算，實際上是對其進行有限元建模分析。下面以SHQ40型三環傳動為例，在SUN工作站上使用I-DEAS軟件中的有限元模塊計算偏心套及齒板的柔度系數。
4.3.1偏心套的有限元柔度計算
偏心套的實體模型如圖4-1所示。由于在三環傳動中，偏心套的兩側是由檔塊整面限制其位移，即有w=0，εz=0，γzy=γzx=0，因此，可以將偏心套簡化為平面應變問題來處理。
圖4-1偏心套實體模型
用I-DEAS文件將實體模型傳輸到有限元分析軟件中。在此幾何模型的基礎上，對外圓周以每360°/5一個節點進行等分，選用平面三角形單元，自動生成如4-2所示的有限元網格圖。
由于偏心套是與高速軸直接套在一起，并通過鍵傳遞扭矩，計算偏心套的柔度時，可取偏心套與鍵接觸處節點法向位移，以及偏心套內圓與軸接觸處各節點的徑向位移為零（見圖4-2所示）。
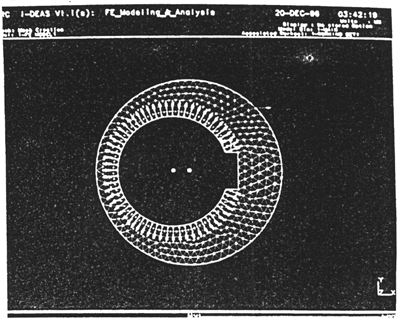
圖4-2偏心套網格及約束圖
齒板是通過軸承將力作用在偏心套的外圓周上，而且在不同的工況其接觸點不相同。因此，計算偏心套的柔度系數矩陣時，需要對外圓周上的每個節點，依次加單位載荷，計算出外圓周上每個節點的位移（亦其柔度系數值）。將這些柔度系數值整理成適合計算調用的磁盤文件PXTRD.DAT。
4.3.2行星齒板的有限元柔度計算
行星齒板在內齒行星傳動中，既是雙曲柄機構的連桿，又是少齒差傳動的內齒輪，是傳遞運動及動力的關鍵零件。齒板一般都是直齒圓柱齒輪。其它零件與其接觸作用的力都是平行于齒板平面沿其厚度均布的。在板面內無任何外力作用，因此可以認為板內各點的六個應力分量中所有沿Z方向（垂直于板聞）的分量均為零，即有σz=τyz=τxz=0,剩下的三個分量σxσyτxy都是作用在和XOY平
面相平行的平面內。行星齒板的實體模型如圖4-3所示。這樣，可以把對齒板的研究簡化成平面應力問題來處理。
行星齒板的實體模型如圖4-3所示。將其傳輸到有限元模塊中，以平面三角形單元進行網格化分，如圖4-4所示。高速軸孔的周邊節點數為360°/Z2。
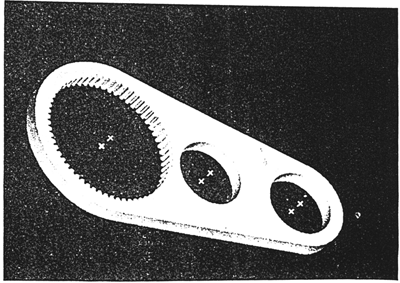
圖4-3齒板實體模型
由于在內齒行齒輪傳動動力分析中，計算的是外力作用點之間的相對位移，因此，在對齒板進行剛體位移約束時，約束水平位移的節點應盡可能選在外力作用點之間的水平坐標范圍之外。約束鉛垂位移的節點應盡可能選在外力作用點之間的垂直坐標之外。這樣才不至于由于約束節點產生的反力影響外力作用點之間的相對位移。根據這個原則，可令齒板最左端邊緣一節點的水平位移為零，以消除齒板的剛體水平位移；令齒板最上端邊緣一節點及中孔垂直對稱軸與齒板最上邊邊緣交點的節點位移為零，以消除齒板的剛體垂直位移和剛體角位移，如圖4-4 所示。
圖4-4齒板網絡及約束圖
單位載荷依次加在各高速軸孔內圓周邊各節點，以及與外齒輪嚙合的內齒圈分度圓節點上，將求解出的柔度系數分為高速軸、內齒圈兩大類，分別見磁盤文件GF1.DAT,GF2.DAT及GFN.DAT，GFN.DAT等。
4.4偏心套和行星齒板的位移及其剛度系數
用有限元法計算出偏心套和齒板的柔度系數表后，就可以由式（4-12）寫出它們在不同工況時，關于嚙合力及軸承作用力的節點柔度方程組。但是，由軸承作用給偏心套及齒板高速軸孔的反力，是沿作用周邊非均布變化的，而且作用范圍（接觸角）也很知道。這給動力分析帶來很大的困難。因此有必要對軸承作用給這兩個零件的節點載荷加以簡化處里。
4.4.1軸承載荷的處理
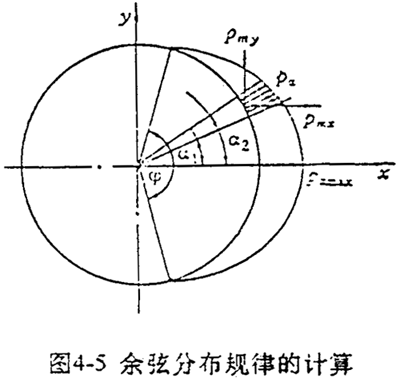
確定作用于結構邊界上的非均布載荷是一件復雜工作，往往需要進行一些較復雜的計算，譬如采用接觸問題有限元法進行計算。在實際應用中常采用一些近似的假設規律來代替這些復雜的未知分布規律。對于軸承載荷，一般假設沿周邊按余弦規律分布如圖4-5所示，即
Pα= Pα maxcos Kα （4-20）
式中Pα二為分布載荷：
Pα max 為最大分布載荷；
由上式可寫出
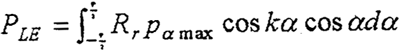
于是得到
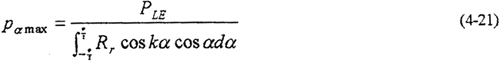
其中PLE為軸承負荷的合力；
Rr為偏心套或齒板孔半徑；
φ為接觸角。
系數K可按下式計算
當α=φ/2時，由式（4-20）得知Pα為零：即Pα=Pα maxcosKα=0
當分布規律求出以后，即可按下式計算接觸邊界上各節點之間微段上分布力的合力Pm及其X、Y軸方向上的分量Pmx和Pmy
然后，按靜力學等效原理，將微段上的合力或其分量分別移置到對應的邊界各節點上。因邊界上各節點之間的微段一般較短，可認為各微段上的作用力近似梯形分布，而Pmx，Pmy就可以認為是作用在梯形的形心上（圖4-6（a））。
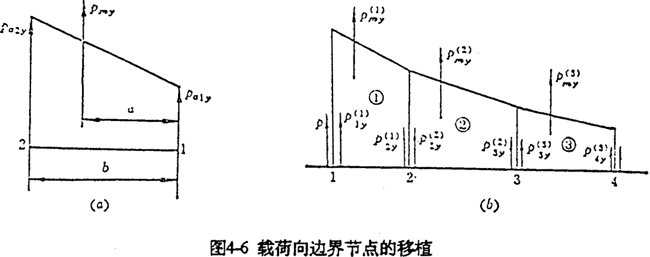
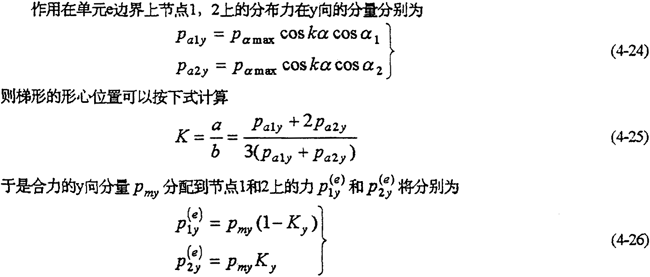
對于邊界上每一個微段，按上述方法計算完后，再對每一個邊界點處的力求和即得到邊界節點沿y向的載荷分量（圖4-6（b））。例如，對于邊界節點2，其節點載荷P2y為
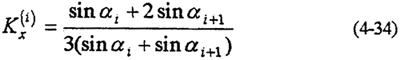
在計算中，接觸角φ的大小是預先給定的，它的大小與接觸處的剛度、間隙以及潤滑情況等因素有關。一般情況下，在120°～180°范圍內選取，本文接觸角取φ=150°計算。
上一頁
下一頁
